Electronics Tour Book

The canonical URL for this site is https://agnd.net/tourbook

1. Introduction

Imagine arriving in a new area / national park / foreign land which is known for its beautiful scenery, dense forests, and more — known as a place where even the natives could spend a lifetime and still have more to experience and learn. My mind’s eye has images of Grand Teton National Park and of New Zeland’s Middle Earth areas; I’ve heard that Tokyo gets a similar sentiment.

Welcome to the field of electronics.

Soon after what seems to be the entrance is a path which seems to branch into two different directions, analog and digital. You would be mistaken to assume that these paths branch off into separate sections, for you would soon find that the trails intersect and branch so much that the distinction is less helpful.

Table 1. Matrix of signal types in time and amplitude
	Continuous Time	Discrete Time
Continuous Amplitude	Analog	switched-capacitor
Discrete Amplitude	neuron spikes	Digital

2. Semiconductor physics

2.1. Introduction

Figure 1. Mountains with fog in the valley near Stoos, Switzerland by Denis Linine from Pixabay

Our tour through semiconductor physics will focus on the main features that are relevant to a circuit designer — those that affect the behavior with respect to voltage and current. The foggy valleys where the underlying quantum-mechanical properties that form the base of these features will be left for a different, more focused, exploration.

2.2. List of Tables

Table 2, “Terms used in semiconductor equations”
Table 3, “Constants for common semiconductors”
Table 4, “Four currents in a semiconductor (A/cm²)”

2.3. Tables and terminology

Table 2. Terms used in semiconductor equations
Symbol	Units	Name
$T$	$\mathrm{K}$	temperature
$E_g$	$\mathrm{J}$ or $\mathrm{eV}$	material bandgap energy
$B$	$\mathrm{cm^{-3}K^{-3/2}}$	material constant
$k_B$	$\mathrm{\dfrac{J}{K}}$ or $\mathrm{\dfrac{eV}{K}}$	Boltzmann constant 1.380 649×10^-23 J/K 8.617 333×10^-5 eV/K
$q$	$\mathrm{C}$	elementary charge 1.602 176 634×10^-19 C
$n_i$	$\mathrm{\dfrac{\#}{cm^3}}$	intrinsic charge carrier density
$n$	$\mathrm{\dfrac{\#}{cm^3}}$	free electron density
$p$	$\mathrm{\dfrac{\#}{cm^3}}$	(free) hole density
$N_D$	$\mathrm{\dfrac{\#}{cm^3}}$	donor doping density
$N_A$	$\mathrm{\dfrac{\#}{cm^3}}$	acceptor doping density
$\mu_n$	$\mathrm{\dfrac{cm^2}{V \cdot s}}$	electron mobility
$\mu_p$	$\mathrm{\dfrac{cm^2}{V \cdot s}}$	hole mobility
$D_n$	$\mathrm{\dfrac{cm^2}{s}}$	electron diffusivity
$D_p$	$\mathrm{\dfrac{cm^2}{s}}$	hole diffusivity

$q \left(N_D + p - N_A - n\right) = 0$

$n \cdot p = n_i^2$

$n = \dfrac{\left(N_D - N_A\right) \pm \sqrt{\left(N_D - N_A\right)^2 + 4 n_i^2}}{2}$

If $\left(N_D - N_A\right) \gg 2 n_i$, then we can approximate $n \approx \left(N_D - N_A\right)$.

$p = \dfrac{n_i^2}{n}$

$p = \dfrac{\left(N_A - N_D\right) \pm \sqrt{\left(N_A - N_D\right)^2 + 4 n_i^2}}{2}$

$n = \dfrac{n_i^2}{p}$

Similarly, if $\left(N_A - N_D\right) \gg 2 n_i$, then we can approximate $p \approx \left(N_A - N_D\right)$.

2.4. Charge carriers

The basic physics of an atom’s structure tells us that electrons are negatively charged and protons are positively charged. Current in amperes is moving charge in coulombs per second. Therefore, current in electronics can be due to electrons moving or protons moving.

Before moving on, here is a reliable saying:

If your protons are moving, you have bigger problems.

Electronics with semiconductors is frequently called “solid-state” for a good reason --- our materials are (all) in the solid state of matter!

Protons moving means your material is in a liquid or, heavin forbid, a gaseous or plasma state. Surely you recognize that this cannot possibly end well :)

Electrons moving is totally fine. In fact, electrons moving in free space between electrodes is fundamentally what is happening in vacuum tubes. The vacuum just ensures that the electrons don’t collide with other (air) molecules while in motion.

This is why the field is called electronics!

Moving positive charges in the form of ions does happen in processes like electrolysis used in electroplating, for example, but that bumps up against chemistry and is out of our scope for now.

Negatively-charged electrons in motion are our only currents. Keep reading for how we fake having positive charges also moving inside semiconductors.

2.4.1. Intrinsic

An intrinsic semiconductor is a material that has no added impurities. Its electrical properties therefore are determined only by the properties of the material itself.

The concentration of thermally-generated electron-hole pairs varies (lots!) with temperature, and is:

\[n_i = B \cdot T^{3/2} \cdot \exp\left(\dfrac{-E_g}{2 k_B T}\right) \;\; \mathrm{\#/cm^3}\]

It is much more common when calculating numbers to need n_i²:

\[n_i^2 = B^2 T^3 \exp{\left(\dfrac{-E_g}{k_B T}\right)}\]

The constant B is derived from material properties related to allowable energy levels an electron can occupy in a crystal.

The law of mass action relates the concentrations of free electrons and holes under thermal equilibrium:

\[n\cdot p = n_i^2\]

This equation holds for all semiconductors. See Wikipedia: Mass action law (electronics) for a short description and more references.

Table 3. Constants for common semiconductors
Semi.	E_g [eV]	B (×10¹⁵) [cm^-3K^-3/2]
Si	1.12	5.2
Ge	0.66	1.66
GaAs	1.42	0.356
GaN	3.49
SiC	3.26

2.4.2. Extrinsic / Doping

Adding impurities to the crystal from Group III or IV elements (replacing an Si atom with another atom such as B or P) also adds extra electrons or holes to the structure.

Dopants which add extra free electrons are called donors, with concentration $N_D \;\; \mathrm{cm^{-3}}$.
Dopants which add extra (free) hole’s are acceptors: $N_A \;\; \mathrm{cm^{-3}}$.

Even when doped, a semiconductor crystal has no net charge. So let’s add up all of the extra charges present in our doped crystal:

\[\sum \text{charges} = q \left( -n +N_D +p -N_A \right) = 0\label{eq-sum-charges}\]

The symbols of equation $\eqref{eq-sum-charges}$ are familiar, but we need to carefully look at the signs of each term:

n: Density of negatively-charged free electrons, including both thermally-generated and extras contributed by donor dopants
N_D: Density of donor dopants. The sign is positive because a donor dopant also contributes a net extra proton along with its extra free electron.
p: Density of positively-charged (free) holes, including both thermally-generated and extras contributed by acceptor dopants
N_A: Density of acceptor dopants. The sign is negative because an acceptor dopant is short a proton in addition to being short an outer-shell electron (a.k.a. hole).

The above charge balance equation, combined with the law of mass action fundamental relationship:

\[n\cdot p = n_i^2\]

allows us to calculate the concentration of free electrons and holes for any doping condition (always choose the $+$ version of the quadratic formula because the density number must be non-negative):

\[n = \dfrac{(N_D - N_A) \pm \sqrt{(N_D - N_A)^2 + 4 n_i^2}}{2} \; \text{ and } \; p = \dfrac{n_i^2}{n}\]

or, solved the other way:

\[p = \dfrac{(N_A - N_D) + \sqrt{(N_A - N_D)^2 + 4 n_i^2}}{2} \; \text{ and } \; n = \dfrac{n_i^2}{p}\]

Q: Are the above two sets of solutions equivalent?

Q: Does it matter which set to use depending on which of $N_D$ or $N_A$ is larger?

When we dope in practice, the impurities $N_D$ and/or $N_A$ are in the range $10^{14} \text{ to } 10^{21} \; \mathrm{cm^{-3}}$, which is much greater than $n_i$ at normal temperatures. Therefore we use the following approximations all the time:

\[\text{when $N_D$ is largest: } n \approx N_D \text{ and } p \approx \frac{n_i^2}{N_D}\]

\[\text{when $N_A$ is largest: } p \approx N_A \text{ and } n \approx \frac{n_i^2}{N_A}\]

Notice how only the minority carrier concentrations are affected by temperature (holes for n-type doping, electrons for p-type doping).

2.4.3. Conclusions

$n_i$ is very sensitive to temperature changes
We can change the concentration of free electrons (n) and (free) holes (p) by doping.
Minority carrier concentrations are greatly affected by temperature. Majority carriers not so much.

2.5. Semiconductor currents

2.5.1. Summary

As usual, we lead with the punchline — results first, then back-fill with its creation story.

Types of charge movement

Drift	constant velocity proportional to E-field
Diffusion	movement from high to low concentration

Two mechanisms of movement with two types of charge carriers yields four types of current in a semiconductor.

Table 4. Four currents in a semiconductor (A/cm²)
	electrons	holes
drift	$\phantom{-} q \cdot n \cdot \mu_n \cdot \vec{E}$	$\phantom{-} q \cdot p \cdot \mu_p \cdot \vec{E}$
diffusion	$\phantom{-} q \cdot D_n \cdot \dfrac{\mathrm{d}\, n}{\mathrm{d} x}$	$- q \cdot D_p \cdot \dfrac{\mathrm{d}\, p}{\mathrm{d} x}$

2.5.2. Drift

2.5.2.1. Physics phundamentals

An electron in an electric field experiences a force.
This force causes the electron (which has mass) to accelerate.
Why does this not therefore cause an increasing current in a material?

Think about this question, then <click to reveal>

The electrons are scattered by the solid — always accelerating but constantly getting knocked off track.

Figure 2. Electron scattering and drift. From https://ece.colorado.edu/~bart/book/book/chapter2/ch2_7.htm#fig2_7_2

Notice in this video during the Plinko game (around 3:00), the camera pans downward at an approximately constant rate: YouTube: The Price is Right former biggest Plinko win primetime.

This results in an average velocity which is constant even though an individual electron is always accelerating.^[1]

The average electron velocity is proportional to the applied E-field.

\[v \propto \vec{E}\]

The constant of proportionality is called mobility (μ_n for electrons and μ_p for holes) and must have units of $\mathrm{\frac{cm^2}{V\cdot s}}$.

For silicon, these values are around:

$\mu_n = 1350 \; \mathrm{\frac{cm^2}{V\cdot s}}$
$\mu_p = \phantom{1} 480 \; \mathrm{\frac{cm^2}{V\cdot s}}$

Recall that the electric potential difference that we commonly name by its units of volts is only and truly the path integral of the electric field. Fortunately, the E-field is a conservative field, so the result of the integration only depends on the end points:

\[\mathrm{V(olts)_{ab}} = - \int_a^b \vec{E}\,dl\]

For holes: $\vec{v}_h = \mu_p \vec{E}$, movement in the same direction as the $\vec{E}$ field vector.
For electrons: $\vec{v}_e = -\mu_n \vec{E}$, movement in the opposite direction as the $\vec{E}$ field vector.

2.5.2.2. Current flow in a bar

Imagine a bar of silicon

Let’s begin by considering the current that flows due to electrons.

Figure 3. Voltage source connected across a (semi)conductor bar.

We know the electron (average) velocity, the density of (free) electrons, and the geometry of the bar.

Notice the double negative! Each negative has a different origin even though the net result is a positive sign.

Let’s normalize this into a current flux by dividing by the cross-sectional area W·h.^[2]

\[J_n = \frac{I_n}{W\cdot h} = \mu_n \vec{E} \cdot n \cdot q\]

J_n has units of $\mathrm{A / cm^2}$ which is the units of a flow per unit area or flux. In an unfortunate naming convention, everyone else calls this term electron current density.

By the same reasoning, we can find the hole current density

\[\begin{align} J_p &= \left(\text{hole velocity}\right) \left(\text{charge density}\right) \\ &= \left(\mu_p \vec{E}\right) \left(p \cdot q\right) \end{align}\]

The total drift current density is then

\[\begin{align} J_{total}(\mathrm{drift}) &= J_n + J_p \\ &= q \left( \mu_n n + \mu_p p \right) \cdot \vec{E} \;\; \mathrm{A/cm^2} \end{align}\]

Finding the current that you would measure with an ammeter from this expression merely requires multiplying by the cross-section area of the bar.

But… look back at Figure 3, “Voltage source connected across a (semi)conductor bar.” and see that we are applying a voltage across the ends of the bar (using an ideal voltage source) — what is $\vec{E}$ ?

An easy-ish way to remember what to do is to recall the units of the electric field: volts per meter. We get our voltage back by multiplying by meters, or the Length of the bar.

\[\vec{E} = \frac{V_{ab}}{L}\]

This only works if the cross-section area is uniform along the length of the bar.

Think about what would happen if the middle of the bar was necked down to a smaller area. KCL forces the current to be constant so therefore {insert thinking here}.

2.5.2.3. Mobility changes with doping :(

Figure 4. Mobility versus doping. From B. Van Zeghbroeck, Principles of Electronic Devices.

B. Van Zeghbroeck, Principles of Electronic Devices

Wayback Machine archive of the pages

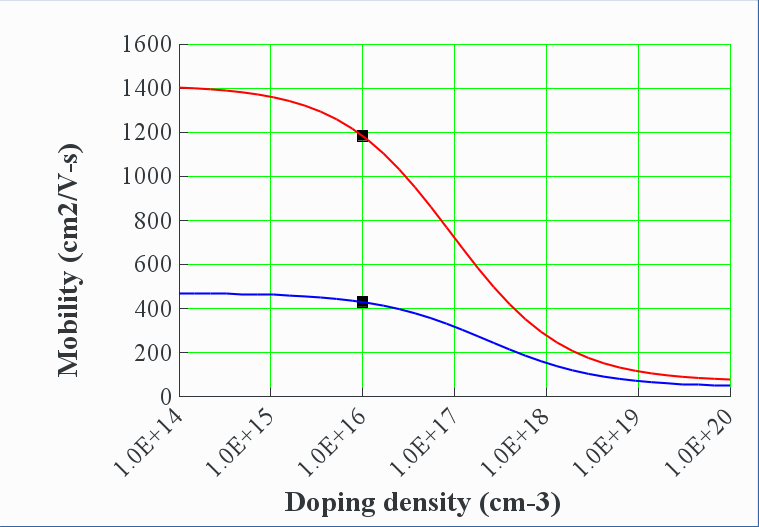
What causes this second-order effect? Does this mean that conductivity decreases with more doping?? <think first, then click to reveal>

More doping means a less uniform crystal and more opportunities for scattering.
But (free) charge density increases faster than mobility decreases, so conductivity still increases.

2.5.2.4. Velocity saturation

It hopefully makes sense that the charge velocity can’t increase so much as to exceed the speed of light, so this is the obvious speed limit. (Light speed is about $3\times 10^{10}\;\mathrm{cm/s}$)

The velocity (therefore current) approaches a lower limit and no longer varies linearly at large E-field strengths (voltage). In a circuit context, this means that the device changes from behaving like a resistor to more like a constant current source.^[3] Velocity saturation is very common in modern integrated circuits.

Figure 5. Drift velocity versus E-field. From Jaeger, Microelectronic Circuit Design

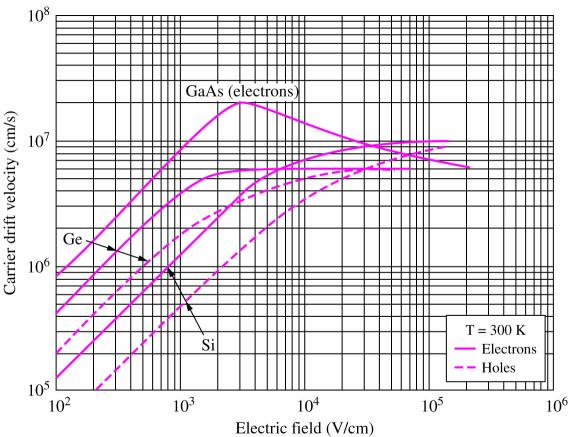
A $130\,\mathrm{nm}$ chip process uses a $1.2\,\mathrm{V}$ supply voltage, giving internal E-fields of

>>> print('%2.2g V/cm' % (1.2 / 130e-9 / 100) )

 9.2e+04 V/cm

which is well within the velocity saturation regime according to Figure 5, “Drift velocity versus E-field. From Jaeger, Microelectronic Circuit Design”.

2.5.3. Diffusion

Figure 6. From Razavi Fundamentals of Microelectronics

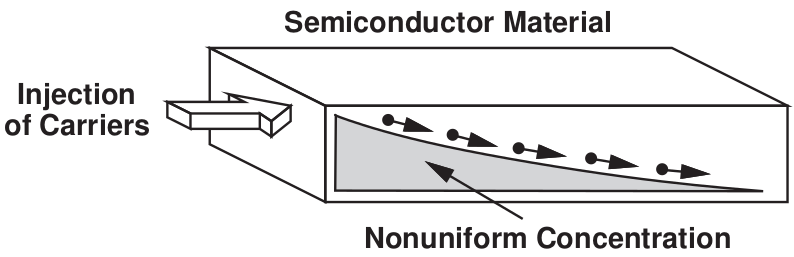
The total diffusion current density is then

\[\begin{align} J_{total}(\mathrm{diff}) &= J_n + J_p \\ &= q \left( D_n \frac{\delta n}{\delta x} - D_p \frac{\delta p}{\delta x} \right) \; \mathrm{A/cm^2} \end{align}\]

Look back at Table 4, “Four currents in a semiconductor (A/cm²)” and match the terms we’ve just worked through. Only one term has a negative sign, hole diffusion, be careful to not make sign errors!

2.6. Junctions

The goal of these subsections is to develop a model of the pn junction that is useful for circuit design and analysis. We will end up with a relationship between current and voltage, and another expression for junction capacitance (charge storage).

2.6.1. pn junction in equilibrium

Figure 7. Semiconductor bar doped half p-type and half n-type

Figure 8. Diode symbol and labels

Imagine taking two separate bars of silicon, one doped to be n-type (N_D) and the other doped to be p-type (N_A). Push these bars together so that there is a single bar where the middle abruptly changes doping types and levels.

At the moment of contact, there is a huge concentration gradient for both holes and electrons. The p-type region with a majority of holes is right next to the n-type region with very few holes and vise versa.

Figure 9. Initial diffusion currents at the junction.

The n and p sides are reversed compared to previous figure. This is to match our other reference materials.

This large gradient causes the holes at the edge of the p region to flow via diffusion to the low concentration side and electrons at the edge of the n region flow via diffusion the opposite direction. Because of the opposite signs for charge polarities and movement direction, the net diffusion current is in the same direction, which is to the left in Figure 9, “Initial diffusion currents at the junction.”.

After a long time, this diffusion will eventually stop because the electron and hole densities have become uniform:

NO !!! We have forgotten about the protons that are in this material!

If your protons are moving, you have bigger problems.

Think about the Group IV dopant atom (say phosphorus) on the n side of the junction. That extra electron (and extra proton!) is in a region of many free electrons and next to a region with few. So it will tend to move (diffuse) to the right towards the p region.

This particular free electron came from the 5^th outer valence electron of the phosphorus dopant atom. Therefore, when it diffuses away, the 15^th proton in the nucleus is left without a charge-balancing mate. We now have a +1 positively-charged phosphorus ion.

Similarly, when the hole contributed by the Group III dopant (say boron) on the p side diffuses to the left, we remember that the hole was filled with an electron. This electron fills the 4^th outer valence “slot” and completes the covalent bonding structure in that area. Don’t forget that boron is short a proton that matched the now-filled hole. Therefore the region has a net −1 negatively-charged boron ion.

Both of these types of ions cannot move because the charges are either a) part of the nucleus, or b) a bound electron. This means that we have:

Charges
      In
    Spaaace ^[4]

or called the depletion region because the volume is eventually depleted of free charge carriers.

Now that there are separated charges, Gauss' law, $\nabla \!\bullet\! \left(\epsilon \vec{E}\right) = Q$, implies that there is a non-zero E-field inside the depletion region. This field is maximum at the boundary between the n and p type doping and, for this example, points to the right.

Recall that the diffusion currents are to the left and the drift current from the E-field is opposite, to the right. Because this semiconductor bar is not connected in a circuit, KCL forces the current at every x location to be zero. The junction is in equilibrium and the drift and diffusion currents must be equal and opposite.

\[\left| J_p(\mathrm{drift}) + J_n(\mathrm{drift}) \right| = \left| J_p(\mathrm{diff}) + J_n(\mathrm{diff}) \right|\]

NO ! (again). The currents must be balanced for holes and electrons individually, or it makes no physical sense.

\[\begin{align} J_p(\mathrm{drift}) + J_p(\mathrm{diff}) &= 0 \\ J_n(\mathrm{drift}) + J_n(\mathrm{diff}) &= 0 \end{align}\]

Take the free electrons equation and substitute their definitions:

\[\begin{align} q \mu_n n \vec{E} &= -q D_n \frac{d n}{dx} \\ - \mu_n n \frac{d V}{dx} &= -D_n \frac{d n}{dx} \\ \end{align}\]

Integrate and divide both sides by n

\[\begin{align} \mu_n \int\limits_b^a dV &= -D_n \int\limits_{n_p}^{n_n} \frac{d n}{n}\\ V(a) - V(b) &= -\frac{D_n}{\mu_n} \ln \left(\frac{n_p}{n_n}\right) \\ \end{align}\]

The left side is the potential difference developed across the depletion region and is given the symbol $V_0$. Also, recall Einstein’s relation, $\frac{D}{\mu} = \frac{k_B T}{q}$, and substitute

\[V_0 = \frac{k_B T}{q} \ln \left(\frac{n_n}{n_p}\right)\]

We usually are only concerned with the magnitude of V₀; notice that swapping the fraction so the majority carriers term (n_n) is in the numerator cancels the leading negative sign. Recognize, for the next section, that the higher potential is on the n side, at location b, given the E-field direction. A similar process can be done to find V₀ from the hole currents.

One final set of substitutions using our (good) approximations of majority and minority carrier concentrations

\[\begin{align} &n_n \rightarrow N_D \\ &n_p \rightarrow \frac{N_A}{n_i^2}\\ \\ V_0 &= \frac{k_B T}{q} \ln \left(\frac{N_A N_D}{n_i^2}\right)\\ &= V_T \ln \left(\frac{N_A N_D}{n_i^2}\right) \end{align}\]

where $V_T$ is called the thermal voltage.

$V_T = \frac{k_B T}{q}$ is something you should memorize.

It is 25.85 mV at 300 K (26.85°C)

Both 25 mV and 26 mV are used in practice for hand calculations at “room temperature.” You will also see 40 = 1/0.025 in equations. Because V_T is usually inside an exponent, the numerical result of a calculation can be sensitive to which approximation you used. Therefore it is best to state your assumptions instead of assuming the reader rounds the same direction as you do.

2.6.2. pn junction in reverse bias

2.6.3. pn junction in forward bias

3. Bipolar transistor operation

Bipolar transistors are named as such because both electrons and holes participate in the device’s operation.

3.1. List of Tables

Table 5, “Transistor parameter definitions”
Table 6, “Bipolar transistor modes”

3.2. pn junction diode review

\[v_C(t) = \left( V_{\mathrm{final}} - V_{\mathrm{initial}} \right) \left[1 - \exp\left(\frac{-t}{\tau}\right)\right] + V_{\mathrm{initial}}\]

A little algebra yields an alternate equation:

\[v_C(t) = V_{\mathrm{final}} + (V_{\mathrm{initial}} - V_{\mathrm{final}})\exp\left(\dfrac{-t}{RC}\right)\]

Figure 10. The Gandalf Diode ensures that you never forget which way current flows in a diode.

3.3. Structure and Physics

Figure Figure 11, “Cross section of a planar BJT” shows the side view of an npn BJT as it would be fabricated on a chip. The order of the three-layer sandwich determines the type (npn or pnp), while the doping level of the outer layers determines the Collector and Emitter terminal labels.

Figure 11. Cross section of a planar BJT

Figure 12. Bipolar current flow in active mode

Where can I read more?

The Wikipedia page Bipolar junction transistor
Lessons In Electric Circuits: Volume III - Semiconductors. Note that this is the exact same content that was later made available at the All About Circuits website.

3.4. Circuit Models

3.4.1. Ebers-Moll model

The Ebers-Moll model is accurate, useful, and therefore well-known. It accounts for normal pn junction current flow and the “transistor action” current flow due to the shared middle region.

Figure 13. Ebers-Moll model for NPN

The diode currents for Figure 13, “Ebers-Moll model for NPN” are found in the normal way by their voltages:

\[\begin{align} I_{ED} &= I_{SE} \left[ \exp\left(\dfrac{v_{BE}}{V_T}\right) - 1 \right] \\ I_{CD} &= I_{SC} \left[ \exp\left(\dfrac{v_{BC}}{V_T}\right) - 1 \right] \end{align}\]

Or, using KCL to find the terminal currents:

\[\begin{align} I_E &= & &I_{ED} & - \alpha_R &I_{CD} \\ I_C &= & \alpha_F &I_{ED} & - &I_{CD} \\ I_B &= & (1-\alpha_F) &I_{ED} & + (1-\alpha_R) &I_{CD} \end{align}\]

If we make the substitution $I_S = \alpha_F I_{SE} = \alpha_R I_{SC}$, the equations become:

\[\begin{align} I_{E} &= & \dfrac{I_S}{\alpha_F} &\left[ \exp\left(\dfrac{v_{BE}}{V_T}\right) - 1 \right] & - I_S &\left[ \exp\left(\dfrac{v_{BC}}{V_T}\right) - 1 \right] \\ I_{C} &= & I_S &\left[ \exp\left(\dfrac{v_{BE}}{V_T}\right) - 1 \right] & - \dfrac{I_S}{\alpha_R} &\left[ \exp\left(\dfrac{v_{BC}}{V_T}\right) - 1 \right] \end{align}\]

Summary to this point: we have a circuit model and set of equations describing the terminal currents given the terminal voltages for a bipolar transistor. There is no notion of operating mode here; this is one set of equations and the rest is plug-and-chug.

Take a minute to also see that the above equations apply equally well to the PNP in Figure 14, “Ebers-Moll model for PNP”.

Figure 14. Ebers-Moll model for PNP

3.4.2. Gummel-Poon model

The [Gummel-Poon] transistor model is an extension of the Ebers-Moll model to better match measurements and other effects. An important aspect is that it accounts for variation in $\beta_{F,R}$ as device current changes. It is the default bipolar transistor model used in SPICE. A listing and brief description of the model’s parameters is at the Wikipedia page Gummel-Poon model.

3.4.3. E-M approximations

Now we will start making some approximations to arrive at some simpler equations. The first is to drop the $-1$’s. Doing this only introduces a significant error when the voltages are within a few multiples of $V_T$, or less than about 100 mV at room temperature.

\[\begin{align} I_{E} &= & \dfrac{I_S}{\alpha_F} &\,\exp\left(\dfrac{v_{BE}}{V_T}\right) & - I_S & \,\exp\left(\dfrac{v_{BC}}{V_T}\right) \\ I_{C} &= & I_S & \,\exp\left(\dfrac{v_{BE}}{V_T}\right) & - \dfrac{I_S}{\alpha_R} & \,\exp\left(\dfrac{v_{BC}}{V_T}\right) \\ I_{B} &= & \dfrac{I_S}{\beta_F} &\,\exp\left(\dfrac{v_{BE}}{V_T}\right) & - \dfrac{I_S}{\beta_R} & \,\exp\left(\dfrac{v_{BC}}{V_T}\right) \\ \end{align}\]

Now, make a few assumptions for the case of an NPN:

The collector is at an equal or higher potential than its emitter, $v_C \ge v_E$.
The base is also at an equal or higher potential than the emitter, $v_B \ge v_E$.

3.4.3.1. Cutoff

Imagine that the base-emitter voltage is near zero (a situation when we can’t ignore the $-1$, remember). The first $v_{BE}$ exponential terms will be also near zero. The second $v_{BC}$ exponential terms will also be near zero or negative. Therefore causing all of the currents to go to zero.

→ This is cutoff mode.

3.4.3.2. Active

Next imagine that the base-emitter voltage is increased until some reasonable amount of current flows through the forward biased base-emitter pn junction — $v_{BE}$ will be around 0.6 V. At the same time, the collector voltage is higher than the base, reverse biasing the base-collector junction. The second exponential terms with $v_{BC}$ will be nearly zero under these conditions and can be ignored.

→ This is forward active mode.

Notice how the collector current is not influenced by the collector voltage.

\[\begin{align} I_E &= \frac{I_C}{\alpha_F} \\ I_C &= I_S \exp\left(\dfrac{v_{BE}}{V_T}\right) \\ I_B &= \frac{I_C}{\beta_F} \end{align}\]

3.4.3.3. Saturation

Finally, keep the base-emitter junction forward biased but keep increasing the current flowing into the base terminal by increasing $v_{BE}$. The collector current will necessarily increase and, in a circuit, the effect will be that the collector’s voltage will decrease. Use Figure 15, “Bipolar transistor internal currents” to consider this situation. The labels will be used in the following discussion to refer to specific current components inside the transistor.

Figure 15. Bipolar transistor internal currents

When the collector voltage is greater than the base voltage (forward active), diode Dbc is reverse-biased and therefore Iy is small enough to ignore. This makes Ib = Ix and Ic = Iz, a condition which holds until the base and collector voltages are equal.

( slow down reading here )

Now increase the base voltage so Iz increases. Remember the earlier relationship between base and collector currents: $i_B = i_C / \beta_F$. This means that Ix and Iz are not independent and Ix = Iz / β_F as well.

Iz is increasing, which is lowering the collector voltage. This causes diode Dbc to become forward biased and start conducting (a little) current. Iy works out to be $\frac{I_S}{\beta_R} \,\exp\left(\frac{v_{BC}}{V_T}\right)$. The collector voltage will end up at a voltage that satisfies KCL at the collector node to make Ic = Iz - Iy. On the base side, you can see that Ib = Ix + Iy.

Is there any combination of $\beta_F$ and $\beta_R$ that allows the collector voltage to drop below the emitter voltage?

The forward biased base-collector junction’s current simultaneously increases the base current and decreases the collector current from their expected values. Since the active mode simplification gives $\beta_F = i_C / i_B$, we make a new version of β for saturation mode:

\[\beta_{\text{sat}} = i_C / i_B\]

For a recap of saturation mode using this new $\beta_{\text{sat}}$, remember that increasing $i_B$ does not increase the collector terminal current Ic (it only increases both Iz and Iy).

You can see this effect by looking at Figure 16 on page 6 of ON Semiconductor’s datasheet for the 2N3904:

Each curve is for a constant collector current (set by an external constant current source).
During the vertical part of each curve, the transistor is in active mode. For example: on the 10 mA curve at $v_{CE} = 1.0\,\mathrm{V}$, the base current is about $80\,\mathrm{\mu A}$ making $\beta_F \approx 125$ in that condition.
As base current increases, the collector voltage does not drop much and approaches 0.1 V.
Take Figure 16 and rotate it 90 degrees counter-clockwise so the plot shows I vs. V.
1. Recall that the base voltage will only increase by 60 mV when the current increases by 10× → in other words consider the base voltage constant.
2. The voltage axis then basically plots the voltage across diode Dbc and its current. Do you see how the collector voltage drops a little to balance KCL at the collector node?

Table 5. Transistor parameter definitions
Term	Name	Definition
$\beta$	common-emitter current gain	$\beta = \dfrac{i_C}{i_B}$
$\alpha$	common-base current gain	$\alpha = \dfrac{i_C}{i_E}$
	relationships	$\beta = \dfrac{\alpha}{1 - \alpha}\\ \alpha = \dfrac{\beta}{\beta + 1}$
$V_T$	thermal voltage	$\dfrac{k_B T}{q} \approx 26\,\mathrm{mV} \text{ at } 300\,\mathrm{K} \text{(room temp)}$
$V_A$	Early voltage	≈ 100V for discrete or 20V on IC
$\beta$	for hand analysis	≈ 100 for discrete or 20 on IC

[AoE] only just mentions Early voltage and refers you to “Chapter 2x” of a (future) supplemental book. See Wikipedia: Early effect for a good description of this phenomenon.

Table 6. Bipolar transistor modes
B-E junction	B-C junction	Mode	Behavior (npn, swap E↔B and E↔C for pnp)
Reverse	Reverse	cutoff	$ \begin{cases} i_C \approx 0 \\ i_B \approx 0 \\ V_{BE} \ll 0.6 V \end{cases} $
Forward	Reverse	active	$ \begin{cases} V_{BE} \approx 0.6 V \\ V_{CE} \rightarrow \text{set by circuit conditions and } > V_{CEsat} \\ i_C = \begin{cases} \alpha \, i_E \text{, or } \approx i_E\\ \beta \, i_B \\ I_S \exp \left( v_{BE} / V_T \right) \end{cases} \\ i_B = i_C / \beta \text{, or } \approx 0\\ \end{cases} $ Figure 16, “npn hand model - no base current” and next
Forward	Forward	saturation	$ \begin{cases} V_{BE} \approx 0.6 V \\ V_{CE} = V_{CE sat} \approx 0.1 V \\ i_C \rightarrow \text{set by circuit conditions and } > 0 \\ i_B \rightarrow \text{must be } > I_C/\beta > 0 \\ (i_E > i_C \text{ by KCL}) \end{cases} $ Figure 20, “npn hand-calculation saturation model” and next
Reverse	Forward	rev-active	(your transistor is in backwards)

3.4.4. Hand-calculation models

There is a section at the end of most chapters in [CMOS VLSI] called “Pitfalls and Fallacies” which gives some hints on where it is easy to over- or under-think an issue. A favorite that applies to this context is:

Using excessively complicated models for manual calculations:

Because models cannot be perfectly accurate, there is little value in using excessively complicated models, particularly for hand calculations. Simpler models give more insight on key trade-offs and more rapid feedback during design.

— [cmosvlsi] section 2.6, page 93

The most important task is to figure out (a.k.a. guess-then-check) which mode the transistor is operating in. Remember that it is the states of the two pn junctions which determine the mode. See the table Table 6, “Bipolar transistor modes” for a summary of these modes and the equations that are useful.

3.4.4.1. (forward) Active mode

Ignoring base current (Β → ∞, α → 0, or i_B → ∞):

Figure 16. npn hand model - no base current

Figure 17. pnp hand model - no base current

Including base current:

Figure 18. npn hand-calculation model - including base current

Figure 19. pnp hand-calculation model - including base current

3.4.4.2. Saturation

Figure 20. npn hand-calculation saturation model

Figure 21. pnp hand-calculation saturation model

3.4.4.3. Example 1 analysis

Figure 22. Example circuit with both collector and emitter resistors

Use the following values with Figure 22, “Example circuit with both collector and emitter resistors”:

VB = 2.0 V
Vcc = 5.0 V
Rc = 1 kΩ
Re = 1 kΩ

Steps to quickly find the DC solution of this circuit:

Guess a mode → active.
Vb is known, so find Ve as 2.0 - 0.6 = 1.4 V.
The voltage across Re is now know, so find Ie as 1.4 V / 1 kΩ = 1.4 mA.
β is large (and $\alpha_F \approx 1$), so just estimate Ic = Ie. This is the model of Figure 16, “npn hand model - no base current”.
This is enough to find the (node) voltage at the collector as (5 V - 1.4 mA × 1 kΩ) = (5 - 1.4) = 3.6 V.
That’s it! … wait, not until we check the mode:
1. Vc > Vb so Q1 is indeed in active mode.
2. Done.

Open up CircuitLab schematic ce-re-example and run a DC Simulation. Click on the nodes and device terminals to see the various node voltages and currents.

Notice that the simulator (which is SPICE underneath) reports the emitter current as negative. It turns out that SPICE defines all device currents as positive into the terminals. Also notice that the current changes sign when probing the current at either end of a resistor. Here also, SPICE uses polarized resistors, which is basically the + and - terminals are defined graphically before simulation.

3.4.4.4. Example 2

Keep the same conditions as above, except change:

Rc ⇒ 10 kΩ

Not much changes on the emitter side of the circuit, so no need to re-do the math.

Find Vc as (5 V - 1.4 mA × 10 kΩ) = (5 - 14.0) = -9.0 V.
The first clue is a negative node voltage when there are no negative supply voltages.
The second is to check the operation mode:
1. Vb > Ve so the B-E junction is forward biased. (no surprise since we forced this)
2. Vc < Vb so the B-C junction is also forward biased. This violates our starting assumption of active mode. The solution is to re-do the problem but assume a different mode (saturation).

Take another swig of coffee and start over. Oh wait, saturation only changes the collector side. All of the emitter side math stays the same.

Set Vce to 0.1 V according to the table.
Therefore Vc is 1.5 V.
Ic calculates to (5.0 - 1.5) / 10 kΩ = 0.35 mA.
If it is useful, we can use KCL to compute the base current as Ie - Ic = 1.05 mA.
The check is to see if base current is larger than what is predicted by $\beta_F$. It is obviously larger than Ic / β, so the check passes.

Check that these numbers are close to what is simulated (which uses the Section 3.4.2, “Gummel-Poon model”) in the same CircuitLab schematic as the first example.

Finally, compute $\beta_{\text{sat}} = 0.35 / 1.40 = 0.25$. This number is useful to see how deep into saturation the transistor is. Here, it is approximately ocean-floor-deep saturation mode.

3.4.5. Rules of thumb

3.4.5.1. Ratio rules

Assuming two transistors are matched (their parameters such as I_S and temperature are exactly the same):

$\dfrac{I_{C2}}{I_{C1}} = \exp\left(\dfrac{\Delta V_{BE}}{V_T}\right)$
$\Delta V_{BE} = V_T \ln\left( \dfrac{I_{C2}}{I_{C1}} \right)$

3.4.5.2. Temperature dependence

[positive emphatic slang here], this is an important topic! IMNSHO, properly dealing with temperature dependence over the entire range of intended operational temperatures separates the professional from the amateur circuit designer.

When talking about your designs:

It just works … always.

— Anyone (except you of course)

It may seem from Section 3.4.5.1, “Ratio rules” that temperature only shows up as $V_T = \frac{k_B\,T}{q}$. Remember that the saturation current I_S is also a strong function of temperature (T⁴ !). The following relationships work well over nearly the entire electronics temperature ranges (very cold is interesting to Physicists, and much hotter and things start melting):

Constant I_C

$\Delta V_{BE} \approx -2.1 \,\mathrm{mV / ^\circ C}$
$\propto 1 / T\,\mathrm{(K)}$

Constant V_BE

$\Delta I_C \approx 9\,\mathrm{\% / ^\circ C}$
$2\!\times I_C \text{ for } \Delta T = 8\,\mathrm{^\circ C}$

4. MOSFET transistor operation

5. Amplifier fundamentals

5.1. List of Tables

Table 7, “Symbol capitalization for circuit quantities”

5.2. Introduction

This chapter discusses the fundamentals of amplifiers and how we talk about and analyze them. These concepts apply to all amplifiers regardless of how they are constructed internally.

What makes this way of thinking about amplifiers so powerful is that we can separate how the the amplifier is used in a larger system from how it is constructed internally. At any given time, a person is only concerned about one of these aspects and can therefore effectively not care about the other.

5.3. Pre-requisites

We start with amplifiers which behave the same at all frequencies. This means that we are ignoring capacitors, inductors, and any frequency-dependence of devices such as transistors.

[LEC] has a well-written tour of this material in Chapters 1 through 10 of Lessons in Electric Circuits: Volume 1 - Direct Current.

Most important to how we view amplifiers are the wonderful concept-tools of Thévenin (mostly) and Norton (some) equivalent circuits. You can find more discussion and worked examples at [CL-book]'s section Thevenin Equivalent and Norton Equivalent Circuits.

Any and all of linear circuit theory is necessary for analyzing amplifiers, especially including:

Components
- Ideal independent and dependent sources: VCVS, VCCS, CCVS, CCCS.
- Resistors, capacitors, inductors.
Techniques for analysis
- Nodal analysis
- Thevenin / Norton equivalent circuits
- Apparent resistance
AC circuits with complex-valued impedances using the Laplace transform

5.4. lower UPPER signal notation

There are several ways to view a circuit besides trying to find the circuit equations directly in the time domain. This is especially terrible difficult when there are semiconductors or other non-linear devices in the circuit besides R, L, C, and sources. To help deal with the complexity, we view circuits from two major perspectives: DC and AC.

Study Table 7, “Symbol capitalization for circuit quantities” for a bit and notice how every current or voltage can be espressed using the “lower_UPPER” notation on the first and last line of the table.

Table 7. Symbol capitalization for circuit quantities
Capitalization	Example	Meaning
lower_UPPER	$v_{BE}(t)$	total quantity, as measured by an oscilloscope with DC coupling
UPPER_UPPER	$V_{BE}$	DC value (average)
lower_lower	$v_{be}(t)$	signal quantity, changes
UPPER_lower	$V_{be}$	complex-valued phasor, a function of frequency
lower_UPPER = UPPER_UPPER + lower_lower	$v_{BE} = V_{BE} + v_{be}$	total signal is average + changes

5.5. AC equivalent circuits

Set all DC independent sources to zero.
- V-sources → short-circuit
- I-sources → open-circuit
Redraw the circuit.

5.6. Small-signal equivalent circuits

Find the AC equivalent circuit.
Decide which inductors and capacitors function as BFCs or BFLs.
Keeping in mind your frequencies of interest, decide to whether to keep or simplify additional inductors and capacitors.
Replace each transistor with its small-signal model.
Re-draw the circuit.

I first learned of the Big Fat Capacitor and Big Fat L (inductor) from Chapter 15 of Thomas Lee’s The Design of CMOS Radio-Frequency Circuits, 2nd ed. (affiliate link)

A BFC is a capacitor whose value has no effect on the frequency response of the circuit by behaving as a short-circuit at all frequencies of interest, while still blocking DC current flow. Similarly, a BFL behaves like an open-circuit at all frequencies of interest, while maintaining a path through it for constant DC current.

These are only for simplifying a discussion or analysis. When you simulate or build a circuit containing a BFC or BFL, you will need to choose an appropriate value. (Watch out for self-resonance and other issues in physical parts!)

6. Bipolar transistor amplifiers

6.1. List of Tables

Table 8, “BJT small-signal parameters”
Table 9, “Definitions for Table Table 10, “Bipolar single-transistor amplifier types””
Table 10, “Bipolar single-transistor amplifier types”

6.2. Introduction

6.3. Tables and terminology

Table 8. BJT small-signal parameters
Symbol	Name	Definition
$g_m$	transconductance	$\dfrac{I_C}{V_T} = \dfrac{\alpha}{r_e}$
$r_e$	intrinsic emitter resistance	$\dfrac{\alpha\, V_T}{I_C} = \dfrac{\alpha}{g_m}$
$r_\pi$	intrinsic base resistance	$\dfrac{\beta\, V_T}{I_C} = \dfrac{\beta}{g_m}$
$r_o$	intrinsic output resistance	$\dfrac{V_A}{I_C}$
$\beta$	alternate	$g_m r_\pi$
$A_0$	intrinsic voltage gain	$g_m r_o = \dfrac{V_A}{V_T}$

Table 9. Definitions for Table Table 10, “Bipolar single-transistor amplifier types”
Symbol	Name
$\boldsymbol{Z}_i$	Impedance looking into transistor input terminal. Does not include the bias network.
$\boldsymbol{Z}_o$	Impedance looking into transistor output terminal. Does not include the bias network.
$A_{v\emptyset}$	Open-circuit voltage gain, no external load attached.
$\boldsymbol{Z}_B$	Impedance of the bias network at the base node looking away from the transistor. Does not include source or load impedances.
$\boldsymbol{Z}_E$	Impedance of the bias network at the emitter node looking away from the transistor. Does not include source or load impedances.
$\boldsymbol{Z}_C$	Impedance of the bias network at the collector node looking away from the transistor. Does not include source or load impedances.
$\boldsymbol{Z}_s$	Output impedance of the source driving the amplifier.
$\boldsymbol{Z}_L$	Load impedance seen by the amplifier.

Table 10. Bipolar single-transistor amplifier types
In	Out	Name	$\boldsymbol{Z}_i$^†	$\boldsymbol{Z}_o$	V-Gain: $\boldsymbol{A_{v\emptyset}}$
B	E	EF emitter follower / CC common-collector	$\left(\beta + 1\right) \left(r_e + Z_E \!\parallel\! Z_L \right)$	$r_e + \dfrac{Z_B \!\parallel\! Z_s}{\left(\beta + 1\right)}$	$\dfrac{\alpha\, Z_E}{r_e + \alpha\, Z_E}$
B	C	CE common-emitter	$\left(\beta + 1\right) \left(r_e + Z_E\right)$	$r_o + (1 + A_0) \bigl(Z_E \parallel \left(r_\pi + Z_B \!\parallel\! Z_s \right) \bigr)$	$\dfrac{-\alpha\, Z_o \!\parallel\! Z_C}{Z_E + r_e}$
E	C	CB common-base	$r_e + \dfrac{Z_B}{\left(\beta + 1\right)}$	$r_o + (1 + A_0) \bigl(Z_E \parallel Z_s \parallel \left(r_\pi + Z_B \right) \bigr)$	$\dfrac{\left\lbrack 1 + A_0 \left(\dfrac{r_\pi}{Z_B + r_\pi}\right)\right\rbrack Z_C}{Z_C + r_o}$
E	B	(not useful)
C	B	(not useful)
C	E	(not useful)
^† $r_o$ is rarely significant here.

Be careful about the definitions in order to properly use the above tables.

Figure 23. Common-Emitter impedances

Figure 24. Common-Collector / Emitter-Follower impedances

Figure 25. Common-Base impedances

6.4. Small-signal models

Figure 26. Bipolar small-signal model connections

Figure 27. Hybrid pi model

Figure 27, “Hybrid pi model” presents the popular hybrid-pi small-signal model of a bipolar transistor for low frequencies.

Figure 28. T model

Figure 28, “T model” is an alternate small-signal model. Be careful of the base current in this model and properly do KCL! Both models will give exactly the same answer — it makes no real difference which one you choose. However, it does sometimes help the analysis / algebra to choose one over the other, depending on the amplifier type. We will use the hybrid pi model most of the time.

6.5. Single transistor amplifiers

6.5.1. Emitter follower / common collector

TODO

Wikipedia: Common collector

6.5.2. Common emitter

TODO

Wikipedia: Common emitter

6.5.3. Common base

TODO

Wikipedia: Common base

6.5.4. Current source

Labeled in AoE Figure 2.40, p.91 as another one of the basic transistor circuits. Mentioned here for completeness, but this is the amplifier chapter.

6.5.5. Switch

The last of the basic transistor circuits in [AoE].

6.6. Two transistor amplifiers

Given the three fundamental amplifier types possible with a transistor, the next extension is to construct amplifiers with two transistors.

CE-CE CE-CB	cascode
CE-EF CB-CE CB-CB CB-EF EF-CE EF-CB	single-ended LTP
EF-EF	Darlington pair

Sziklai pair

7. Differential pairs

7.1. List of Tables

7.2. Bipolar differential pair

Figure 29. Basic bipolar differential pair

We first start our foray into the world of differential circuits by considering the basic bipolar differential pair in Figure 29, “Basic bipolar differential pair”.

Set the two input voltages to zero.

What is the emitter voltage v_E? (think of the answer before revealing!)

The base voltages are the same because they are set to be so, the emitter voltages are the same because they are attached to the same node.

v_BE is about 0.6 V, so v_E is about −0.6 V

This is not a problem so far, but what happens when V1 and V2 are not equal? Is this even possible? How can V1 be anything different if v_BE is supposed to always be 0.6 V?

Wait a second: why “must” v_BE be 0.6 V in the first place?

It is merely an approximation of the base-emitter voltage in active mode that causes collector currents somewhere around 1 mA at around room temperature (300 K).

This connection forces us to use a more accurate approximation for the collector current, see Table: Bipolar transistor modes:

\[i_E = \dfrac{i_C}{\alpha} = \dfrac{I_S}{\alpha} \exp\left(\frac{v_{BE}}{V_T}\right)\]

KCL forces the emitter currents to sum to I_tail. A substitution for each transistor’s current gives us:

\[I_{tail} = \frac{I_{S2}}{\alpha_2} \exp\left(\frac{v_{BE2}}{V_{T2}}\right) + \frac{I_{S2}}{\alpha_2} \exp\left(\frac{v_{BE2}}{V_{T2}}\right)\]

So many currents and voltages — take a minute to list out which are actually transistor properties and not part of the circuit analysis, but just have units of V or A.

$I_{S1}$ and $I_{S2}$ — depend on individual doping, geometry, and other manufacturing variations (and junction temperature)
$V_{T1}$ and $V_{T2}$ — thermal voltage $k_B T / q$, transistors may be at different temperatures!

Since the emitters are connected together, we can write the base-emitter voltages as

$v_{BE1} = v_1 - v_E$
$v_{BE2} = v_2 - v_E$

Assumptions

To proceed much more and arrive at the important result of this path, we need to make two assumptions:

Both transistors are at the same temperature.
The transistors are matched, meaning:
- $I_{S1} = I_{S2} = I_S$, and
- $\alpha_1 = \alpha_2 = \alpha$
Then, purely and only for convenience, we’ll approximate $\alpha \approx 1$

Now, factor the common v_E term out of the exponentials.

\[I_{tail} = I_S \exp\left(\frac{-v_E}{V_T}\right) \left[\exp\left(\frac{v_1}{V_T}\right) + \exp\left(\frac{v_2}{V_T}\right) \right]\]

and rearrange for later use

\[I_S \exp\left(\frac{-v_E}{V_T}\right) = \frac{I_{tail}}{\exp\left(\frac{v_1}{V_T}\right) + \exp\left(\frac{v_2}{V_T}\right)}\]

Follow this progression for the collector current in transistor Q1 (each step is simple!):

\[\begin{align} i_1 &= I_S \exp\left(\frac{v_{BE1}}{V_T}\right) \\ &= I_S \exp\left(\frac{v_1}{V_T}\right) \exp\left(\frac{-v_E}{V_T}\right) \\ & \\ &= I_S \exp\left(\frac{-v_E}{V_T}\right) \exp\left(\frac{v_1}{V_T}\right) \\ & \\ &= \dfrac{I_{tail} \exp\left(\frac{v_1}{V_T}\right)}{\exp\left(\frac{v_1}{V_T}\right) + \exp\left(\frac{v_2}{V_T}\right)} \end{align}\]

Then multipy by “1,” an algebra trick that is handy in many situations:

\[\begin{align} i_1 &= \dfrac{I_{tail} \exp\left(\frac{v_1}{V_T}\right)}{\exp\left(\frac{v_1}{V_T}\right) + \exp\left(\frac{v_2}{V_T}\right)} \cdot \dfrac{\exp\left(\frac{-v_1}{V_T}\right)}{\exp\left(\frac{-v_1}{V_T}\right)} \\ & \\ &= \dfrac{I_{tail}}{1 + \exp\left(\frac{-(v_1 - v_2)}{V_T}\right)} \\ \end{align}\]

Figure 30. Generating single-ended voltages from DM and CM terms

7.2.1. Differential pair / long-tailed pair

7.2.1.1. Half-circuit analysis

Figure 31. Common-mode half-circuit

Figure 32. Differential-mode half-circuit

8. Operational amplifiers

8.1. List of Tables

8.2. Cascaded amplifiers

Dave Jones of EEVblog does a good job of walking through the design decisions for his uCurrent GOLD low current measurement tool: EEVblog #572 - Cascading Opamps For Increased Bandwidth

Cascaded amplifiers animations

9. Tools

This section holds a collection of links to tools hosted here and elsewhere which are useful for work in electronics.

Voltage divider resistor calculator - agnd.net

E-series standard values (pdf) - Vishay.

The ECE department has the following passive parts

All E12 resistor values from 1 Ω to 10 MΩ with 5% tolerance.
All E6 capacitor values from 100 pF to 100 μF in overlapping types.
E3 capacitor values from 10 pF—100 μF and 100 μF—1000 μF.

Index

Section 3.2, “pn junction diode review”

References

[[[341-notes]]] D. White, ECE 341 Class notes 2019 folder, https://drive.google.com/drive/folders/1vzdLxzTUAC6xXF6YjVcDRuy_BKR7gzDz?usp=sharing
[[[341-docs]]] D. White, ECE 341 reference documents folder, https://drive.google.com/folderview?id=0B5O5cSaA0tEQYVpaSnJxMGFrdHM
[AoE] P. Horowitz and W. Hill, The Art of Electronics 3rd ed. (affiliate link), Cambridge University Press, 2015. https://artofelectronics.net
[L-AoE] T. Hayes, Learning the Art of Electronics: A Hands-On Lab Course (affiliate link), Cambridge University Press, 2016. https://learningtheartofelectronics.com
[LEC] Tony R. Kuphaldt, Lessons in Electric Circuits, Source version: https://www.ibiblio.org/kuphaldt/electricCircuits/, All About Circuits version: https://www.allaboutcircuits.com/textbook/
[CL-book] Michael F. Robbins, CircuitLab, Ultimate Electronics: Practical Circuit Design and Analysis, https://www.circuitlab.com/textbook/
[TCA] Alfred D. Gronner, Transistor Circuit Analysis, Simon & Schuster, 1970, https://archive.org/details/TransistorCircuitAnalysis
[CMOS VLSI] Neil Weste and David Harris, CMOS VLSI Design - A Circuit and Systems Perspective, 4th edition. Addison-Wesley, 2011. http://pages.hmc.edu/harris/cmosvlsi/4e/index.html
[Guidebook] D. White, Guidebook for Electronics II. https://agnd.net/valpo/341/guidebook
[Gummel-Poon] H.K. Gummel, H.C. Poon, An Integral Charge Control Model of Bipolar Transistors. Bell System Technical Journal, 49: 5. May-June 1970 pp 827-852. https://archive.org/details/bstj49-5-827
[ROHM] ROHM Semiconductor, Electronics Basics, http://www.rohm.com/web/global/en_index
[vishay-e-series] Vishay, Standard Series Values in a Decade for Resistances and Capacitances, https://www.vishay.com/docs/28372/e-series.pdf

Electronics Tour Book by Dan White is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Permissions beyond the scope of this license may be available by contacting the author.
Comments and suggestions are very welcome!

1. and therefore also creating a magnetic field!

2. Everyone else calls J “current density,” but the quantity is flow / area, which is a flux in my book (and the customary term from calculus).

3. that still absorbs energy

4. (not) The Muppets

Symbol	Units	Name
\(T\)	\(\mathrm{K}\)	temperature
\(E_g\)	\(\mathrm{J}\) or \(\mathrm{eV}\)	material bandgap energy
\(B\)	\(\mathrm{cm^{-3}K^{-3/2}}\)	material constant
\(k_B\)	\(\mathrm{\dfrac{J}{K}}\) or \(\mathrm{\dfrac{eV}{K}}\)	Boltzmann constant 1.380 649×10^-23 J/K 8.617 333×10^-5 eV/K
\(q\)	\(\mathrm{C}\)	elementary charge 1.602 176 634×10^-19 C
\(n_i\)	\(\mathrm{\dfrac{\#}{cm^3}}\)	intrinsic charge carrier density
\(n\)	\(\mathrm{\dfrac{\#}{cm^3}}\)	free electron density
\(p\)	\(\mathrm{\dfrac{\#}{cm^3}}\)	(free) hole density
\(N_D\)	\(\mathrm{\dfrac{\#}{cm^3}}\)	donor doping density
\(N_A\)	\(\mathrm{\dfrac{\#}{cm^3}}\)	acceptor doping density
\(\mu_n\)	\(\mathrm{\dfrac{cm^2}{V \cdot s}}\)	electron mobility
\(\mu_p\)	\(\mathrm{\dfrac{cm^2}{V \cdot s}}\)	hole mobility
\(D_n\)	\(\mathrm{\dfrac{cm^2}{s}}\)	electron diffusivity
\(D_p\)	\(\mathrm{\dfrac{cm^2}{s}}\)	hole diffusivity

Symbol	Name	Definition
\(g_m\)	transconductance	\(\dfrac{I_C}{V_T} = \dfrac{\alpha}{r_e}\)
\(r_e\)	intrinsic emitter resistance	\(\dfrac{\alpha\, V_T}{I_C} = \dfrac{\alpha}{g_m}\)
\(r_\pi\)	intrinsic base resistance	\(\dfrac{\beta\, V_T}{I_C} = \dfrac{\beta}{g_m}\)
\(r_o\)	intrinsic output resistance	\(\dfrac{V_A}{I_C}\)
\(\beta\)	alternate	\(g_m r_\pi\)
\(A_0\)	intrinsic voltage gain	\(g_m r_o = \dfrac{V_A}{V_T}\)

In	Out	Name	\(\boldsymbol{Z}_i\)^†	\(\boldsymbol{Z}_o\)	V-Gain: \(\boldsymbol{A_{v\emptyset}}\)
B	E	EF emitter follower / CC common-collector	\(\left(\beta + 1\right) \left(r_e + Z_E \!\parallel\! Z_L \right)\)	\(r_e + \dfrac{Z_B \!\parallel\! Z_s}{\left(\beta + 1\right)}\)	\(\dfrac{\alpha\, Z_E}{r_e + \alpha\, Z_E}\)
B	C	CE common-emitter	\(\left(\beta + 1\right) \left(r_e + Z_E\right)\)	\(r_o + (1 + A_0) \bigl(Z_E \parallel \left(r_\pi + Z_B \!\parallel\! Z_s \right) \bigr)\)	\(\dfrac{-\alpha\, Z_o \!\parallel\! Z_C}{Z_E + r_e}\)
E	C	CB common-base	\(r_e + \dfrac{Z_B}{\left(\beta + 1\right)}\)	\(r_o + (1 + A_0) \bigl(Z_E \parallel Z_s \parallel \left(r_\pi + Z_B \right) \bigr)\)	\(\dfrac{\left\lbrack 1 + A_0 \left(\dfrac{r_\pi}{Z_B + r_\pi}\right)\right\rbrack Z_C}{Z_C + r_o}\)
E	B	(not useful)
C	B	(not useful)
C	E	(not useful)
^† \(r_o\) is rarely significant here.

	electrons	holes
drift	\(\phantom{-} q \cdot n \cdot \mu_n \cdot \vec{E}\)	\(\phantom{-} q \cdot p \cdot \mu_p \cdot \vec{E}\)
diffusion	\(\phantom{-} q \cdot D_n \cdot \dfrac{\mathrm{d}\, n}{\mathrm{d} x}\)	\(- q \cdot D_p \cdot \dfrac{\mathrm{d}\, p}{\mathrm{d} x}\)

Term	Name	Definition
\(\beta\)	common-emitter current gain	\(\beta = \dfrac{i_C}{i_B}\)
\(\alpha\)	common-base current gain	\(\alpha = \dfrac{i_C}{i_E}\)
	relationships	\(\beta = \dfrac{\alpha}{1 - \alpha}\\ \alpha = \dfrac{\beta}{\beta + 1}\)
\(V_T\)	thermal voltage	\(\dfrac{k_B T}{q} \approx 26\,\mathrm{mV} \text{ at } 300\,\mathrm{K} \text{(room temp)}\)
\(V_A\)	Early voltage	≈ 100V for discrete or 20V on IC
\(\beta\)	for hand analysis	≈ 100 for discrete or 20 on IC

Capitalization	Example	Meaning
lower_UPPER	\(v_{BE}(t)\)	total quantity, as measured by an oscilloscope with DC coupling
UPPER_UPPER	\(V_{BE}\)	DC value (average)
lower_lower	\(v_{be}(t)\)	signal quantity, changes
UPPER_lower	\(V_{be}\)	complex-valued phasor, a function of frequency
lower_UPPER = UPPER_UPPER + lower_lower	\(v_{BE} = V_{BE} + v_{be}\)	total signal is average + changes

Symbol	Name
\(\boldsymbol{Z}_i\)	Impedance looking into transistor input terminal. Does not include the bias network.
\(\boldsymbol{Z}_o\)	Impedance looking into transistor output terminal. Does not include the bias network.
\(A_{v\emptyset}\)	Open-circuit voltage gain, no external load attached.
\(\boldsymbol{Z}_B\)	Impedance of the bias network at the base node looking away from the transistor. Does not include source or load impedances.
\(\boldsymbol{Z}_E\)	Impedance of the bias network at the emitter node looking away from the transistor. Does not include source or load impedances.
\(\boldsymbol{Z}_C\)	Impedance of the bias network at the collector node looking away from the transistor. Does not include source or load impedances.
\(\boldsymbol{Z}_s\)	Output impedance of the source driving the amplifier.
\(\boldsymbol{Z}_L\)	Load impedance seen by the amplifier.