Faraday says that changing magnetic flux induces a voltage, let’s see this!

1. Setup

1.1. Materials

  • 47 μH toroidal inductor

    • Alternative: 100 μH axial inductor from the Analog Parts Kit (top markings 101)

  • 100 Ω resistor

  • Analog Discovery 2

1.2. Objectives

Determine the mutual inductance dot orientation for an inductor coupling its field to an added coil of wire.

Concepts

  • Inductor i-v relationship

  • Mutual inductance dot convention

  • Coupled flux and coil turns

2. Procedure

2.1. Build initial circuit

lab12 sch
Figure 1. Initial schematic
lab12 connections
Figure 2. Breadboard connections

Construct the circuit of Figure 1 so it looks similar to Figure 2. Oscilloscope input channel 1 is shown measuring the voltage across R1 in the picture. This setup allows you to measure:

  • Inductor voltage

  • Inductor current (by Ohm’s law)

  • Wavegen #1 signal voltage

Setup the waveform generator with the following configuration:

  • square

  • 100 kHz

  • 1 Vp-p

Attach the input channels so that your scope displays:

  • Inductor voltage.

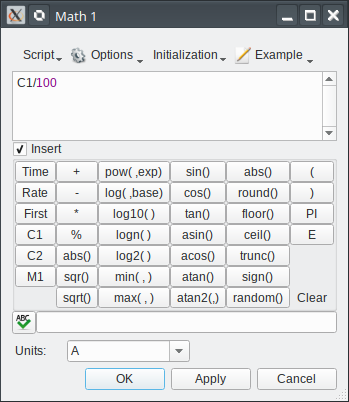
  • Inductor current. Do this by adding a Math ("Custom") display that computes Cx/100 where x is the channel you have measuring VR. See Figure 3 — be sure to change the units!

lab12 math current
Figure 3. Custom math channel in Waveforms

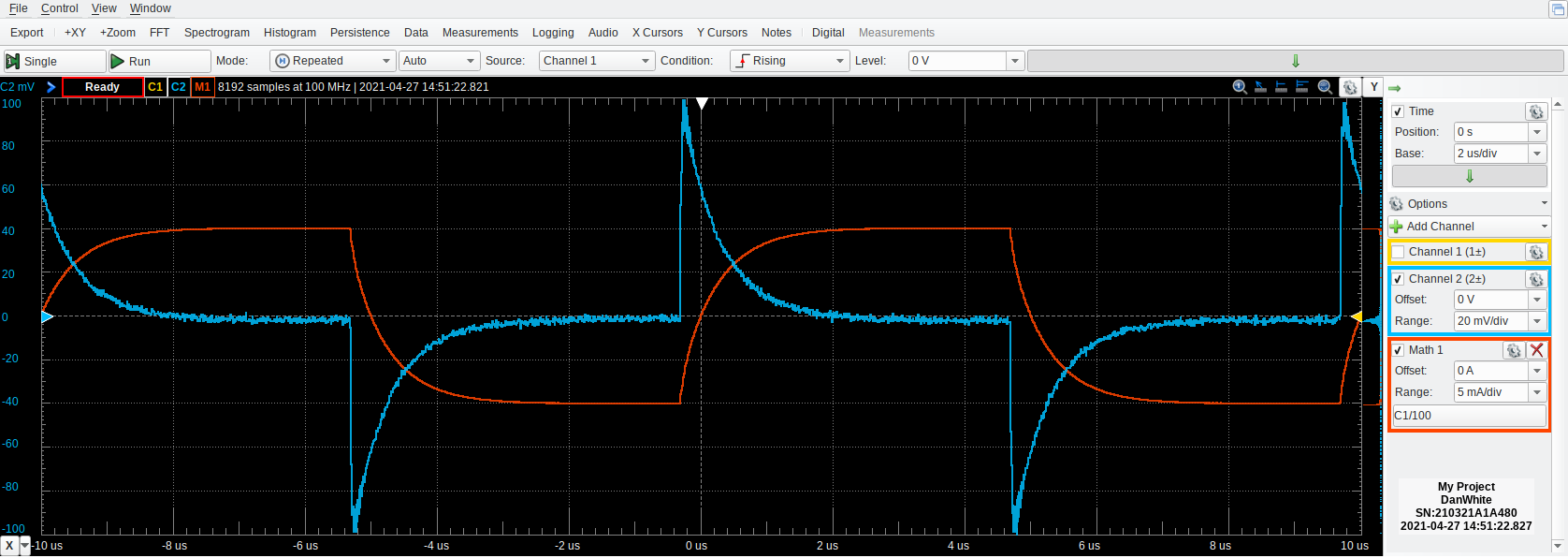
Carefully look at the two (voltage and current) waveforms associated with this inductor.

  • Relate the displayed waveforms to the inductor equation relating voltage to current.[1]

You should be able to make a reasonable estimate of the inductance from the time-domain waveforms. Describe your measurements, calculations, and result.

2.2. Coupled magnetic field

lab12 loop1
Figure 4. Single coupled loop
lab12 mutual
Figure 5. Schematic view of magnetically-coupled loop

Now thread a wire through the center of the inductor as shown in Figure 4. The schematic view of this setup in Figure 5 reminds you that you now have two inductors which share some portion of their magnetic fields. This is measured either as M mutual inductance or k coupling coefficient.

Change your scope inputs to measure the current through the L1 inductor and the voltage across the inductor (the added wire) Loop. The current flowing through L1 generates a magnetic flux (the many turns of wire increase the generated flux by N for the same current). The other wire (green in the picture) intercepts this flux. Because the flux is changing, Faraday’s law says that there is a voltage induced across the second coil that is proportional to the derivative of this magnetic flux.

  • Figure 5 includes a dot for one of the inductors. Experimentally determine which end of your loop has the dot by carefully considering the polarities of the L1 current, the polarity of the Loop voltage, and the direction of the windings (remember the right-hand rule).

Carefully keep track of which end is which for both inductors!

Draw and annotate sketches of your setup to help keep the orientations straight.
lab12 scope
Figure 6. Waveforms Scope view of induced voltage and inductor current

2.3. Adding loops

lab12 loop2
Figure 7. Two coupled loops
lab12 loop2alt
Figure 8. Alternative inductor two loop coupling

Add a second turn to your coupled inductor by passing your wire through the center of L1 again similar to Figure 7.

This coil has two complete turns. The connection to the scope input completes the full turn.

  • Determine the relationship between the coil’s induced voltage (peak-to-peak is a good metric) and the number of turns.

Plot this relationship!

3. Submission

Write a report that describes your lab setup. It must inclue discussion about each of the [ ] checkbox items.

Include:

  • schematics representing each setup

  • pictures of the physical setup

  • documentation of all your measurements, including units

  • mathematical work as needed

Discussion engineering style involves measurements, math, and numbers and provides reality and observation-based reasoning for claims; no "truth by assertion."

1. \(v_L = L \dfrac{d I_L}{dt}\) and \(i_L = \dfrac{1}{L}\int\limits_0^t v_L\!(\tau)\, d\tau + i_L(0^-)\)