1. Supplies

  • Analog Discovery 2

  • breadboard

  • 3× "jellybean" pnp transistors

  • 3× "jellybean" npn transistors

  • 3× 10 kΩ resistors

  • 47 Ω resistor

  • 10 Ω resistor

  • 50 kΩ potentiometer

  • 470 pF capacitor (small ceramic). (OK to be ±1 value increment)

2. Review formulas

2.1. Filters

1-pole RC high-pass filter:

\[H_{HP}(f) = \dfrac{j\dfrac{f}{f_H}}{1 + j\dfrac{f}{f_H}} \quad\text{with}\quad f_H = \dfrac{1}{2\pi R C}\]

1-pole RC low-pass filter:

\[H_{LP}(f) = \dfrac{1}{1 + j\dfrac{f}{f_H}} \quad\text{with}\quad f_H = \dfrac{1}{2\pi R C}\]

2.2. Op-amp DC response

\[v_{OUT} = v_{in}\underbrace{\left(\frac{A_{v0}}{1 + A_{v0} \dfrac{R_1}{R_1 + R_2}}\right)}_\text{gain} + \underbrace{\biggl(V_{OS} + I_{B+} R_{eq+} - I_{B-} R_{eq-}\biggr)\left(\frac{A_{v0}}{1 + A_{v0} \dfrac{R_1}{R_1 + R_2}}\right)}_\text{offset} \label{dcout}\]

If you make the following assumptions:

  • The open-loop gain Av0 is large enough, which means \(\gg \left(1 + \frac{R_2}{R_1}\right)\)

  • The opamp’s open-loop output impedance Zout is low enough, or much less than the impedance seen by the output node (for this lab = 50 047 Ω). (the above equation \(\eqref{dcout}\) already sets \(Z_{out} \rightarrow 0\))

The total non-inverting opamp output from the input signal and DC errors VOS and (IB, IOS) ←→ (IB+, IB-) is:

\[v_{OUT} = v_{in}\underbrace{\left(1 + \dfrac{R_2}{R_1}\right)}_\text{gain} + \underbrace{\biggl(V_{OS} + I_{B+} R_{eq+} - I_{B-} R_{eq-}\biggr)\left(1 + \dfrac{R_2}{R_1}\right)}_\text{offset}\]

  • \(R_{eq+}\) and \(R_{eq-}\) are the impedances seen by the + and - input terminals of the opamp.

2.3. Op-amp AC response

Most opamps have a dominant pole frequency response shape, where one pole dominates the response with the other poles and zeros near or obove than the unity-gain frequency fT.

The handout from day28 (Wednesday) discrete-opamp-ss-analysis.pdf

opamp lab6 sim
Figure 1. Simulation circuit

Use the following CircuitLab setup:

CircuitLab: opamp-lab6-sim_math

The opamp model in CircuitLab conveniently allows us to set the main datasheet parameters directly, without needing to find a device part number that mostly matches. Very handy for what if experimentation.

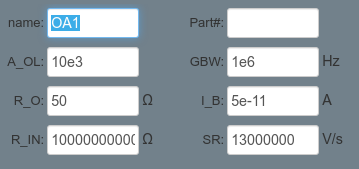
opamp lab6 sim settings
Figure 2. Op-amp model values

Simulate the frequency response of this circuit at various positions of the potentiometer’s wiper, parameter Rp.K (fraction of rotation 0…​1).

One key result of the small-signal analysis is that the lower, dominant, pole frequency is located at

\[f_{p1} = \frac{1}{R_1 C_c G_{m2} R_2}\]

and that the Gain-Bandwidth Product (GBW) is approximately

\[\mathrm{GBW} = \frac{G_{m1}}{C_c}\]

This \(G_{m1}\) is simply the transconductance of the input differential transistor pair, which is directly proportional to bias current

\[G_{m1} = g_{m1,2} = \frac{I_{\mathrm{tail}}}{V_T}\]

Increasing GBW requires either

  • Increasing the tail current, and therefore the power supply current drawn by the opamp.

  • Decreasing Cc, which has a lower limit to maintain stability when under negative feedback.

3. Procedure

alt
Figure 3. Discrete opamp schematic
opamp lab6
Figure 4. Variable gain non-inverting amplifier

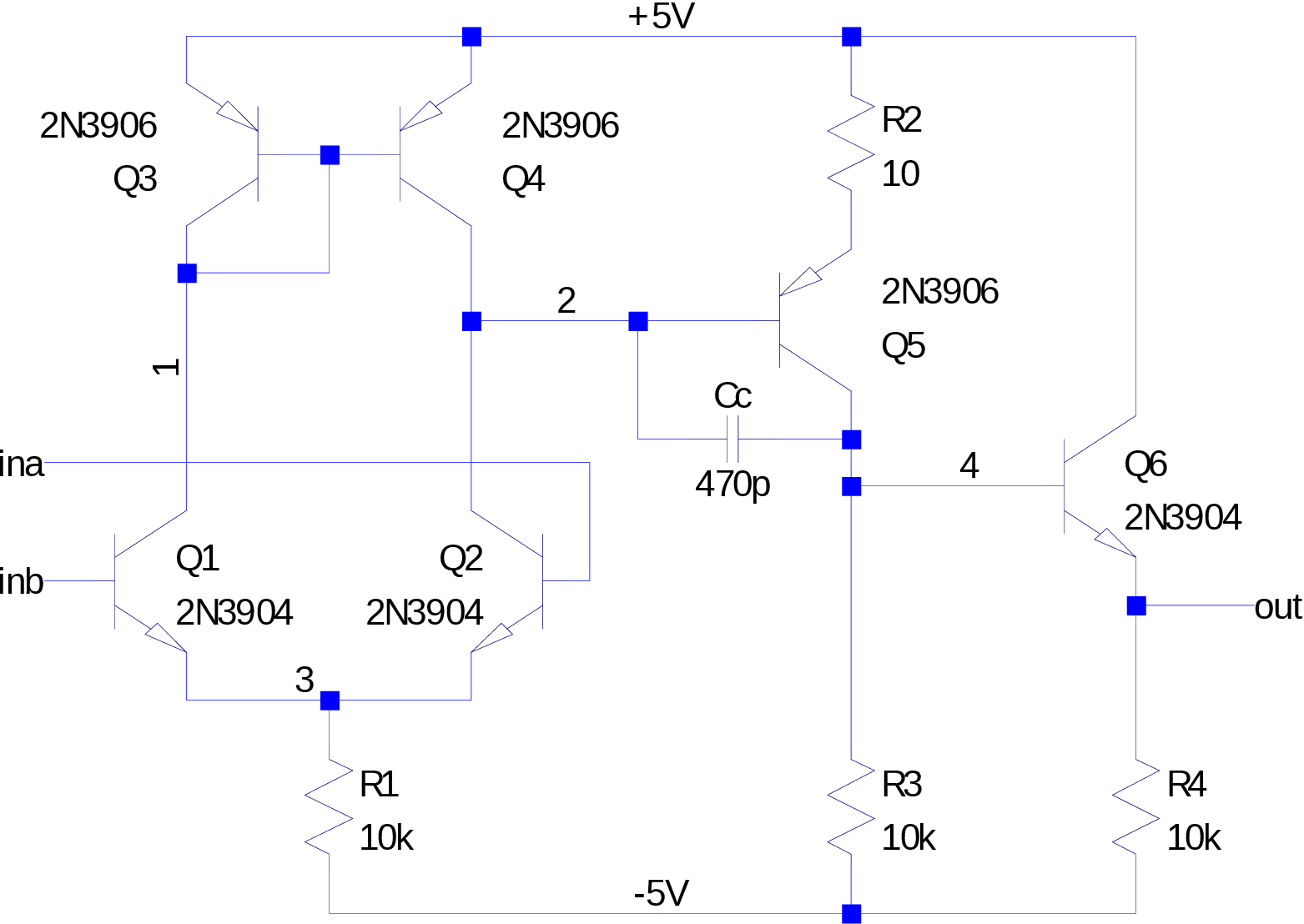
Construct your Lab 5 opamp of Figure 3. Then use this as a normal “triangle” opamp and construct the circuit of Figure 4. Instrument this circuit with your AD2 with the connections shown.

You can alternatively make your op amp using the MC3346 npn transistor array. Or make a pnp-input version. The important part is to have the same Itail current and a known value for compensation capacitor C_C.

Open WaveForms and startup the Wavegen and Scope panels.

Setup the system so the amplifier output is a 1 Vp-p, 1 kHz sinusoid centered around 0 V and is operating at a gain of 100 V/V (adjust the potentiometer).

Make note of the W1 input amplitude.

Verify that the amplifier is operating correctly with a clean output waveform centered near 0 V.

Open the Network panel in WaveForms and set it up with the following parameters:

  • Upper row settings

    • Scale: Logarithmic

    • Start: 100 Hz

    • Stop: 10 MHz

    • Samples: 100

  • Right side settings

    • WaveGen: set to the same offset and amplitude as the current WaveGen values

    • Magnitude

      • Units: dB

      • Top: 70 dB

      • Bottom: 0 dB

    • Phase

      • Offset: -90°

      • Range: 180°

☆ This setup plots the magnitude and phase of your amplifier’s transfer function!

Verify that the low frequency gain is still 100 V/V, remember the conversions between dB and linear voltage units:

  • \(\text{gain (dB)} = 10 \log_{10} \Big\lbrack(\text{V/V})^2\Big\rbrack\)

  • \(\text{gain (V/V)} = \sqrt{10^{\text{(dB)}/10}}\)

or, simplified to the perhaps more familiar form:

  • \(\text{gain (dB)} = 20 \log_{10} \Big\lbrack\text{(V/V)}\Big\rbrack\)

  • \(\text{gain (V/V)} = 10^{\text{dB}/20}\)

The frequency response plot is only valid when the system is linear, meaning the input and output signals are all within proper ranges to not clip or otherwise be distorted. One nice way to check this is to turn on the oscilloscope view at the same time. Do this by selecting menu item View  Time.

Vary the potentiometer to set your amplifier to several low-frequency gains and measure your amplifier’s -3 dB frequency. Also compute the gain-bandwidth product at each setting (GBW is computed with gain in linear units, not dB).

Gain (dB) fH (-3 dB) GBW (MHz)

0

10

20

30

40

50

60
Notice the following characteristics of these measurements

  • When low-frequency gain increases, the bandwidth decreases by the same proportion.

  • GBW is relatively constant.

  • GBW is nearly the same as the unity gain (1 V/V, 0 dB) frequency, fT.

  • The phase is -45° at the -3 dB frequency, exactly as predicted by the transfer function math.

4. Old lab notes for reference

[ the below is here simply for your edification and extra information that may be useful ]

Construct the opamp of Figure 3 on a small section of breadboard. The capacitor Cc helps to stabilize this amplifier, but you can greatly help the situation by minimizing the length of jumper wires in the construction.

  • Be sure to allow yourself easy access for replacing capacitor Cc and for attaching meters to nodes ina, inb, and out.

  • Use the physically small ceramic capacitor types for Cc.

  • Add a large capacitor (1 to 10 μF) between the Vcc and Vee nodes to help reduce the effect of the long wires connecting to the power supply.

  • For each of the 3 npn transistors: use the “diode check” mode on the multimeters to measure VBE. Select the transistors with the closest values as Q1 and Q2. Since VBE is sensitive to temperature changes, it is best to minimize touching the transistors until you’ve measured them (use pliers).

  • Do a similar procedure to select your Q3 and Q4 pair.

alt
Figure 5. Compact construction example
alt

See Figure 5 for an example of pre-bending transistor leads and building the circuit in the same general arrangement as the schematic. This makes troubleshooting easier since the geometry is similar and reduces the parasitic inductances and the electric and magnetic coupling between nodes and loops.

alt
Figure 6. Vertical
resistor

Several of the resistors are bent to be in a vertical position. Bend and trim your resistor leads as shown in Figure 6. The right lead in the figure makes for a convenient loop for attaching probes.

References