2021-09-20
Floating point in IEEE 754 format
-
What is the computer architecure (hardware / software / algorithmic / etc.) reason for the ordering of the fields in '754 format?
sign : exponent : fraction -
The signed exponent field is encoded using a bias, why is it done that way instead of just 2’s complement?
IEEE 754 single-precision (32 bit)

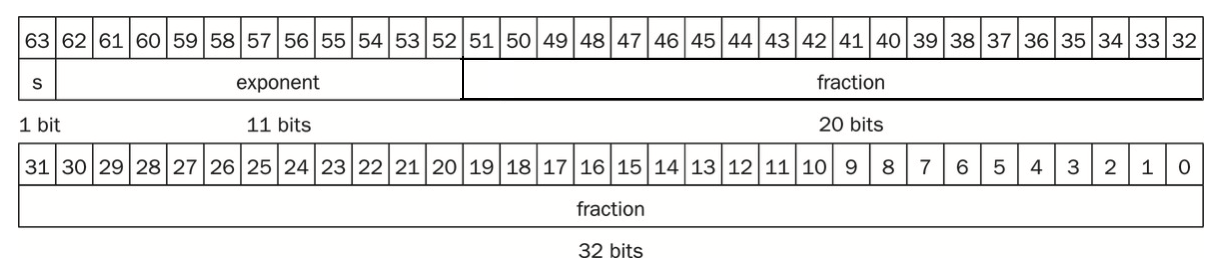
IEEE 754 double precision (64-bit)
Meaning of the bits to construct the binary point number: \((-1)^s \; 1.F \times 2^{E-bias}\)
There is always a leading 1. in the fraction, so it isn’t encoded into the bit representation.
Hardware to do arithmetic (+, -, ×, ÷, compare) is … a whole 'nother topic!
Fixed point
There is a thing called fixed point where arithmetic is done using a binary point somewhere inside the N-bit number.
0b1111.1111 is Q4.4 format.
while 0b1.101 0101 is Q1.7 format.
An integer ALU can be used for fixed point arithmetic with some additional software housekeeping for keeping track of the binary point. It is somewhat common in DSP implementations since it is generally faster than using full IEEE 754 floating point hardware. In this case, it is up to the programmer to keep track of the binary point! (The programmer then writes functions and other tools to help out.)
Nowadays, you can buy a "floating point DSP" which does have a speed-optimized FPU. Programming DSP algorithms on such devices is much easier than a fixed-point DSP.
In class exercise
Decoding 1
Consider the following 32-bit value:
0001 1001 1000 0101 1000 0111 0011 0111

%%
hex 0x19858737 int 428181303 decimal 1.38064905242e-23 computed 1.3806490524162535742025823474237659731211902425229709479026496410369873046875E-23 **** %%
-
Convert to hex:
-
Value if considered an unsigned integer
-
Value if considered a signed (32-bit) integer
-
Value if considered a 32-bit IEEE 754 single precision float
-
If this was a constant in some code, what well-known symbolic physical constant would this be?
-
.
Decoding 2
Another 32-bit value:
1010 0000 0011 1101 0010 0110 1101 0001

%%
SI exact 1.602 176 634 e-19 hex 0xa03d26d1 uint 2688362193 int32 -1606605103 decimal -1.602 176 597 46 e-19 computed -1.6021765974585869277149415869365700615389869199134409427642822265625E-19 **** %%
-
Convert to hex:
-
Value if considered an unsigned integer
-
Value if considered a signed (32-bit) integer
-
Value if considered a 32-bit IEEE 754 single precision float
-
If this was a constant in some code, what well-known symbolic physical constant would this be?
-
Is 32 bits enough precision to properly encode this constant without rounding error according to SI