Lesson 11 - Magnetic Fields

Figure 1. Well-known people in the field of electricity and magnetism

1. Curl

\[\mathop{curl} \vec{A} = \vec{\nabla} \times \vec{A}\]

It is helpful, as the book points out also, to view the curl as a dot product of the field along a closed path (think: circular) around a point.

\[\mathop{curl} \vec{A} = \lim_{\Delta s \rightarrow 0} \frac{\hat{a}_n \oint \vec{A} \bullet \mathrm{d}\vec{l}}{\Delta s}\]

Figure 2. Book Figure 11.1

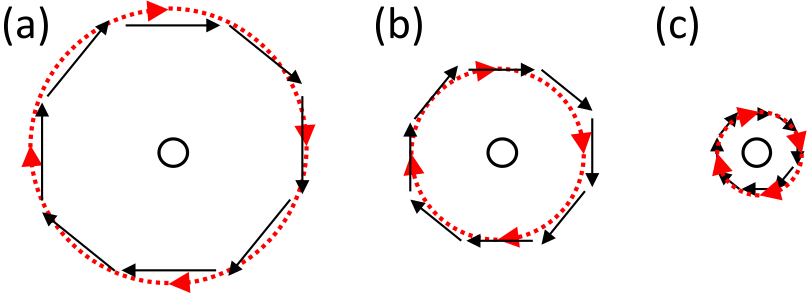
What is the direction of the curl of the field in Figure 2?

You were admonished to not memorize book Equation 11.4, but it is worth a brief look while Figure 2 is still in view.

\[\mathop{curl} \vec{A} = \left(\frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z}\right) \hat{a}_x + \left(\frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x}\right) \hat{a}_y + \left(\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y}\right) \hat{a}_z \label{curl}\]

Choose a point on the red ▶ path around (b). For ease, choose a cardinal direction, imagining a “normal” x-y plane with the circle centered on the origin.
For a right-handed cartesian coordinate system, the z axis is facing out of the page towards you.
The black arrows represent the \(\vec{A}\) vector field’s magnitude and direction at that point.
Use equation \(\eqref{curl}\) to determine the direction of the resulting vector.

Work through this with a partner, then click to see one solution

If we assume that the field does not vary in the z direction (like rotating cylinders), then the solution goes as follows for the six partial derivatives:

Curl component in the \(\vec{a}_x\) direction:
1. The \(A_z\) component is zero, so the partial is also zero.
2. \(A_y\) is constant along the z direction, so zero.
3. Therefore there is no x-direction curl component.
Curl component in the \(\vec{a}_y\) direction:
1. \(A_x\) is constant along the z direction, so zero.
2. The \(A_z\) component is zero, so this partial is also zero.
3. Therefore there is no y-direction curl component.
Curl component in the \(\vec{a}_z\) direction:
1. \(A_y\) is negative, and doesn’t change much when moving in the +x direction. Call this “±small”.^[1]
2. \(A_x\) on the x-axis is zero, but as we move in the +y direction the x component definitely increases. So the result is positive.
3. (“±small” − positive) is negative ^[2]
Therefore the curl of this vector field is in the \(-\hat{a}_z\) direction, or into the page away from the reader. Curl, as defined, is a right-handed thing, so use your right hand’s fingers to curl around in the direction of the red ▶ path and see where your thumb is pointing.

2. Magnetic things

but we start with the flux density this time.

\(\mathbf{\vec{B}}\)	magnetic flux density. In units of teslas (T), which are ??? per square meter.
\(\mathbf{\mathrm{Wb}}\)	weber. Magnetic flux (same difference between I and J for current(density)). Units of \(\mathrm{A \cdot s}\).

\(\mathrm{T = \frac{Wb}{m^2}}\)

1 gauss = 10^-4 tesla

Magnetic fields do not have a source nor a sink. (!)

→ the divergence of the magnetic flux density is zero.

μ₀ is no longer defined as \(4\pi \times 10^{-7} \, \mathrm{H/m}\) and is instead a measured quantity, though the two are equal for their first 9 significant digits.

See 2019 redefinition of the SI base units for the rest of the story.

2.1. Magnets

magnetic domains are regions in ferromagnetic materials.

“permanent magnets can be destroyed by heating them to high temperatures”: This is the Curie temperature. It is important to be aware of this value when using magnets or inductors.

The North pole is the end where field lines flow out.

2.2. Solenoids

The formula given for a solenoid in the Chapter 11 Summary is for a single-layer coil. Very Few coils actually have only one layer of windings IRL.

3. Ampere’s Law

v0.1

\[\oint \vec{B} \bullet \mathrm{d}\vec{l} = \mu_0 \cdot I_{\mathrm{enc}}\]

\[\vec{\nabla} \times \vec{B} = \mu_0 \cdot \vec{J}\]

1. To fit with Ampere’s Law, the y component gets smaller as we move away from the origin, but this isn’t what is implied in the picture (go from (b) to (a) and notice how the black downwards arrow gets longer). So perhaps the figure needs to be updated to fit typical circulating fields in this chapter?

2. Oh my, is this engineer-grade mathematics or what? So jank. But the students in this course are engineers, so everyone just thinks such a thing is reasonable.