Semiconductor: Drift current

1. Review

\[n = \dfrac{(N_D - N_A) \pm \sqrt{(N_D - N_A)^2 + 4 n_i^2}}{2} \;\text{ and }\; p = \dfrac{n_i^2}{n}\]

1.1. When to approximate?

We as Engineers use approximations all the time. They make calculations easier or less complex, while still being accurate enough for the purpose.

But how do you know what is “close enough”?

The key skill is being aware of how much precision is needed for the final result or design. For example:

The clock’s frequency needs to be within ±X % so the timer is off by less than 1 second per day. (compute this X value!)
The amplifier’s gain needs to be 10±1 V/V.
The diode’s forward voltage at 25 °C and 1 mA of current needs to be 650 mV ±1%.

The Razavi book only uses the approximation and skips even showing the accurate formula for charge carrier density with doping. Assume that N_A = 0 and the material is only doped with donors.

\[\begin{equation} n \approx N_D \;\text{ and }\; p \approx \frac{n_i^2}{N_D} \end{equation}\]

So, when can you use the approximation for an error less than X%?

One nice way to figure this out is to come up with a relationship between the size of the variables that, when true, let you safely use the easy equation.

For less than 1% error, N_D should be (less/greater) than compared to n_i. Compute this condition.

2. Current in semiconductors

This content is mirrored at Electronics Tour Book - 2.5. Semiconductor currents.

How is drift current constant instead of accelerating?: Youtube: The Price is Right former biggest Plinko win - start at 2:49

2.1. Summary

As usual, we lead with the punchline — results first, then back-fill with its creation story.

Types of charge movement

Drift	constant velocity proportional to E-field
Diffusion	movement from high to low concentration

Two mechanisms of movement with two types of charge carriers yields four types of current in a semiconductor.

Table 1. Four currents in a semiconductor (A/cm²)
	electrons	holes
drift	\(\phantom{-} q \cdot n \cdot \mu_n \cdot \vec{E}\)	\(\phantom{-} q \cdot p \cdot \mu_p \cdot \vec{E}\)
diffusion	\(\phantom{-} q \cdot D_n \cdot \dfrac{\mathrm{d}\, n}{\mathrm{d} x}\)	\(- q \cdot D_p \cdot \dfrac{\mathrm{d}\, p}{\mathrm{d} x}\)

2.2. Drift

2.2.1. Physics phundamentals

An electron in an electric field experiences a force.
This force causes the electron (which has mass) to accelerate.
Why does this not therefore cause an increasing current in a material?

Think about this question, then <click to reveal>

The electrons are scattered by the solid — always accelerating but constantly getting knocked off track.

Figure 1. Electron scattering and drift. From https://ece.colorado.edu/~bart/book/book/chapter2/ch2_7.htm#fig2_7_2

Notice in this video during the Plinko game (around 3:00), the camera pans downward at an approximately constant rate: YouTube: The Price is Right former biggest Plinko win primetime.

This results in an average velocity which is constant even though an individual electron is always accelerating.^[1]

The average electron velocity is proportional to the applied E-field.

\[v \propto \vec{E}\]

The constant of proportionality is called mobility (μ_n for electrons and μ_p for holes) and must have units of \(\mathrm{\frac{cm^2}{V\cdot s}}\).

For silicon, these values are around:

\(\mu_n = 1350 \; \mathrm{\frac{cm^2}{V\cdot s}}\)
\(\mu_p = \phantom{1} 480 \; \mathrm{\frac{cm^2}{V\cdot s}}\)

Recall that the electric potential difference that we commonly name by its units of volts is only and truly the path integral of the electric field. Fortunately, the E-field is a conservative field, so the result of the integration only depends on the end points:

\[\mathrm{V(olts)_{ab}} = - \int_a^b \vec{E}\,dl\]

For holes: \(\vec{v}_h = \mu_p \vec{E}\), movement in the same direction as the \(\vec{E}\) field vector.
For electrons: \(\vec{v}_e = -\mu_n \vec{E}\), movement in the opposite direction as the \(\vec{E}\) field vector.

2.2.2. Current flow in a bar

Imagine a bar of silicon

Let’s begin by considering the current that flows due to electrons.

Figure 2. Voltage source connected across a (semi)conductor bar.

We know the electron (average) velocity, the density of (free) electrons, and the geometry of the bar.

Notice the double negative! Each negative has a different origin even though the net result is a positive sign.

Let’s normalize this into a current flux by dividing by the cross-sectional area W·h.^[2]

\[J_n = \frac{I_n}{W\cdot h} = \mu_n \vec{E} \cdot n \cdot q\]

J_n has units of \(\mathrm{A / cm^2}\) which is the units of a flow per unit area or flux. In an unfortunate naming convention, everyone else calls this term electron current density.

By the same reasoning, we can find the hole current density

\[\begin{align} J_p &= \left(\text{hole velocity}\right) \left(\text{charge density}\right) \\ &= \left(\mu_p \vec{E}\right) \left(p \cdot q\right) \end{align}\]

The total drift current density is then

\[\begin{align} J_{total}(\mathrm{drift}) &= J_n + J_p \\ &= q \left( \mu_n n + \mu_p p \right) \cdot \vec{E} \;\; \mathrm{A/cm^2} \end{align}\]

Finding the current that you would measure with an ammeter from this expression merely requires multiplying by the cross-section area of the bar.

But… look back at Figure 2 and see that we are applying a voltage across the ends of the bar (using an ideal voltage source) — what is \(\vec{E}\) ?

An easy-ish way to remember what to do is to recall the units of the electric field: volts per meter. We get our voltage back by multiplying by meters, or the Length of the bar.

\[\vec{E} = \frac{V_{ab}}{L}\]

This only works if the cross-section area is uniform along the length of the bar.

Think about what would happen if the middle of the bar was necked down to a smaller area. KCL forces the current to be constant so therefore {insert thinking here}.

2.2.3. Mobility changes with doping :(

Figure 3. Mobility versus doping. From B. Van Zeghbroeck, Principles of Electronic Devices.

B. Van Zeghbroeck, Principles of Electronic Devices

Wayback Machine archive of the pages

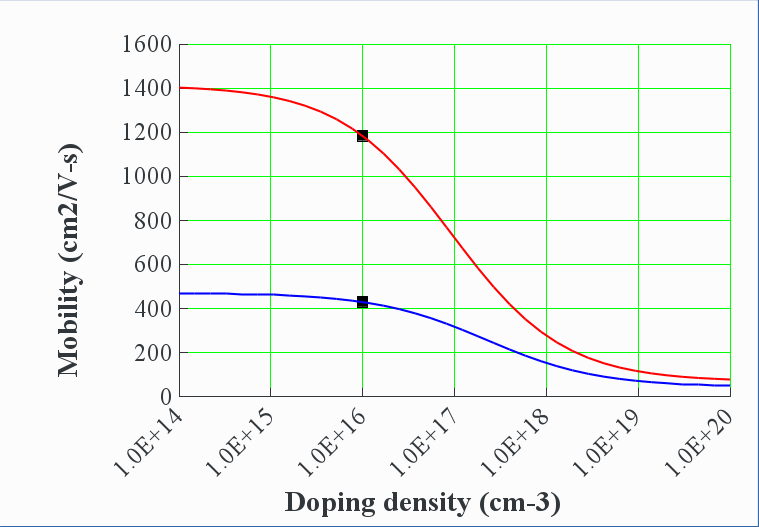
What causes this second-order effect? Does this mean that conductivity decreases with more doping?? <think first, then click to reveal>

More doping means a less uniform crystal and more opportunities for scattering.
But (free) charge density increases faster than mobility decreases, so conductivity still increases.

2.2.4. Velocity saturation

It hopefully makes sense that the charge velocity can’t increase so much as to exceed the speed of light, so this is the obvious speed limit. (Light speed is about \(3\times 10^{10}\;\mathrm{cm/s}\))

The velocity (therefore current) approaches a lower limit and no longer varies linearly at large E-field strengths (voltage). In a circuit context, this means that the device changes from behaving like a resistor to more like a constant current source.^[3] Velocity saturation is very common in modern integrated circuits.

Figure 4. Drift velocity versus E-field. From Jaeger, Microelectronic Circuit Design

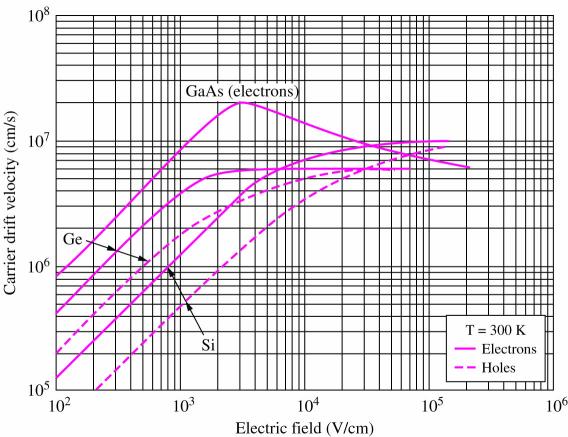
A \(130\,\mathrm{nm}\) chip process uses a \(1.2\,\mathrm{V}\) supply voltage, giving internal E-fields of

>>> print('%2.2g V/cm' % (1.2 / 130e-9 / 100) )

 9.2e+04 V/cm

which is well within the velocity saturation regime according to Figure 4.

1. and therefore also creating a magnetic field!

2. Everyone else calls J “current density,” but the quantity is flow / area, which is a flux in my book (and the customary term from calculus).

3. that still absorbs energy