1. Review

The reading of Razavi section 2.2.1 was assigned and expected to have been completed by the start of this class session. Also §2.2.2, but your reading assignments are intentionally ahead of class time topics.

Tourbook table: Four currents in a semiconductor

Symbol Name Units

V

n

p

μn

μp

kB

ni

ND

N~A

W, h, d
Charge carriers of interest

  • e-

  • h+

Charges move by

  • Electric field → \(\mathrm{V(olts)_{ab}} = - \int_a^b \vec{E}\,dl\)

2. Diffusion

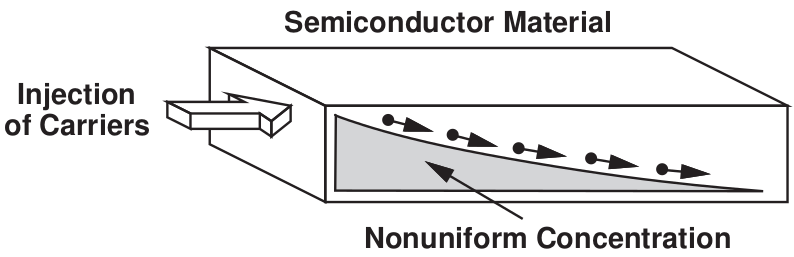
razavi fig2 11
Figure 1. From Razavi Fundamentals of Microelectronics
current diffusion electron
Figure 2. Electron diffusion current density
current diffusion hole
Figure 3. Hole diffusion current density

The total diffusion current density is then

\[\begin{align} J_{total}(\mathrm{diff}) &= J_n + J_p \\ &= q \left( D_n \frac{\delta n}{\delta x} - D_p \frac{\delta p}{\delta x} \right) \; \mathrm{A/cm^2} \end{align}\]
Look back at our four currents in a semiconductor and match the terms we’ve just worked through. Only one term has a negative sign, hole diffusion, be careful to not make sign errors!

2.1. Einstein relation

\[\dfrac{D_n}{\mu_n} = \dfrac{k_B T}{q}\]
\[\dfrac{k_B T}{q} = V_T \; \text{ thermal voltage}\]