Practice ⇒ experience ⇒ knowledge

1. Common emitter amplifier

ce amp
Figure 1. Generic common-emitter amplifier

1.1. DC solution

Given

  • Vcc = 10 V

  • Rload = 10 kΩ

  • Rs = 50 Ω

Want

  • IC1 = 1 mA

  • VC = 60% of Vcc

  • VE about 1× to 2× the value of VBE

Select


The rounded R values affect the actual DC solution:

  • VB =

  • IC1 =

  • VC =

  • VE =

Then compute the small-signal transistor values:

  • gm = =

  • rπ = =

  • re = =

  • ro = =

1.2. Small-signal circuit

  • Find the AC equiv circuit

  • Decide what to do with the reactive components. The capacitors don’t have a value, for the purpose here, assume that they are BFCs[1].

Then find the input impedance, output impedance, and (voltage) gain of the small-signal circuit.

2. Complex Ohm’s Law

Using proper names lessens confusion.

impedance
admittance

By the definitons of impedance and reactance:

\[Z_x = \frac{V_x}{I_x} \; \text{and} \; Y_x = \frac{I_x}{V_x}\]

BUT

\[G \ne \frac{1}{R},\;\text{nor does}\; B \ne \frac{1}{X} \; \text{in general}\]

Go back to day10 — Why this “impedance about equal” relationship? and read the section, follow the step-by-step mathematical manipulation to help you remember how to deal with complex numbers.

  • What is the impedance of a capacitor? ZC=

  • What is the impedance of an inductor? ZL=

3. Yamaha PM-1000 Channel Equalizer

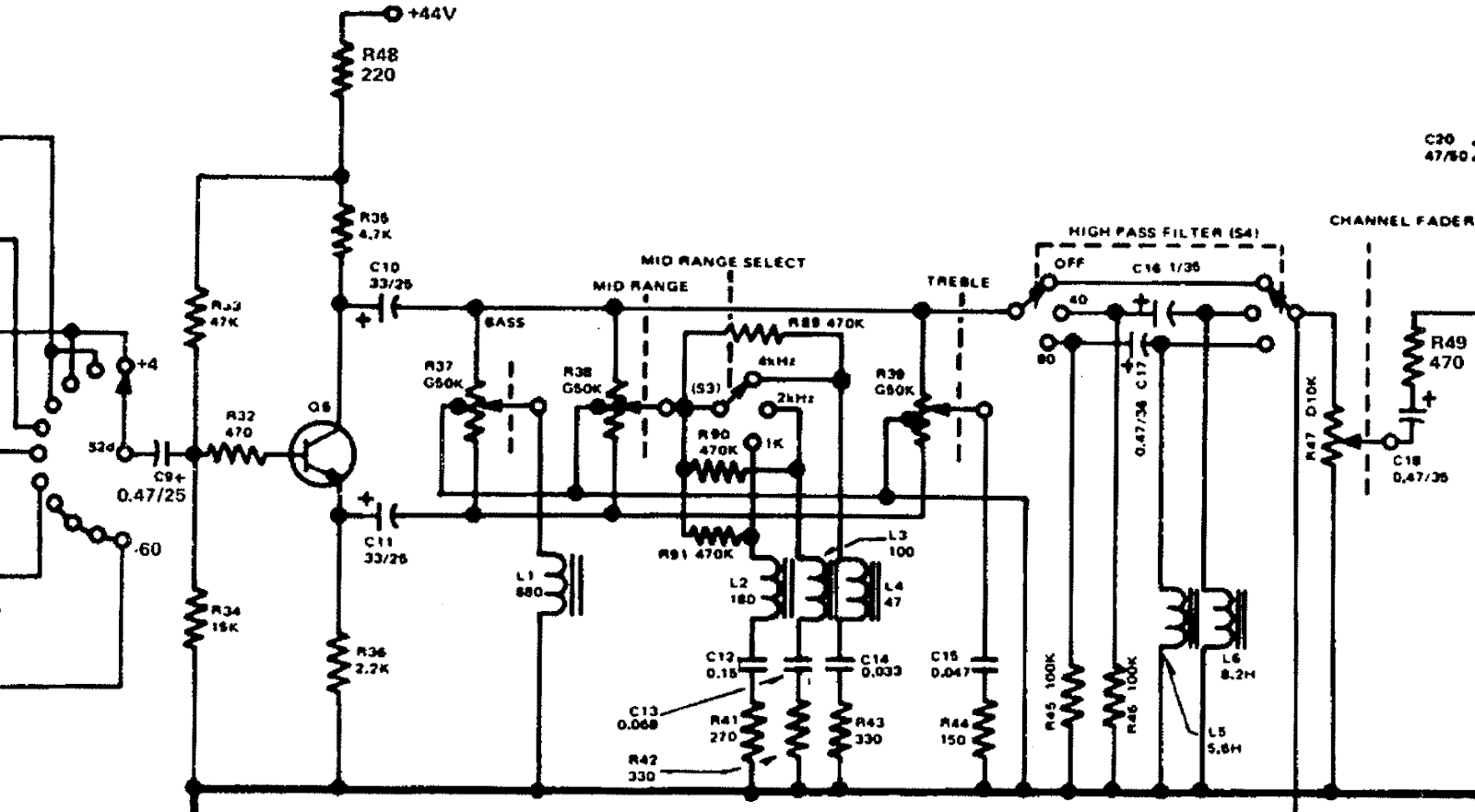
pm1000 eq

3.1. Step 1a

Draw the AC equivalent circuit.
Pretty easy, you may decide to skip the redrawing part.

3.2. Step 1b

  • Decide a position for each of the two switches Mid range select (S3) and High pass filter (S4). For visual ease, leave them in the same position as the schematic: 4 kHz and OFF.

  • Decide a position for each of the three potentiometers R37, R38, and R39. → Set them all to the middle position.

These are four-terminal potentiometers instead of the more familiar three-terminal devices. The 4-term versions were somewhat popular in the era when analog equalizer circuits like this were popular. Now, they are special-order parts.

Quite simply, the 4th terminal is a static “center tap” along the resistive track that the movable wiper rides along.

In this circuit, the center-taps are all connected to the zero reference node.[2] Therefore, when the potentiometer knob is set to the middle position, the wiper is also connected to zero. This leaves only 25 kΩ from each of the upper and lower connections to zero.

E.g. the node connected to the minus terminal of C11 effectively has three, 25 kΩ resistors in parallel to zero and similarly for the right side of C10.

3.3. Step 2

Decide what to do with any inductors and capacitors.

  • Capacitors C9, C10, and C11 remain in the circuit.

  • What are the frequencies of interest?
    As a full-range audio circuit, use 20 Hz — 20 kHz.

  • Compute the reactance of these capacitors at the lowest frequency of interest.

Details
\[\begin{align} X_9 = \frac{1}{2\pi\, 20 \cdot 0.47\mu} \approx 17\,\mathrm{k\Omega} \\ X_{10, 11} = \frac{1}{2\pi\, 20 \cdot 33\mu} \approx 240\,\mathrm{\Omega} \\ \end{align}\]

The reactance of C10 and C11, even at the lowest frequency of interest, is ten times smaller than the connected resistances.

Make your own decision then click
Decision:

Approximate C10 and C11 as short-circuits.

Capacitor C9's reactance is close to the value of R34, which forms a high-pass filter with a corner frequency apparently close to 20 Hz. At higher frequencies, the high(er) signals pass through the filter, meaning C9 has little additional influence.

Make your own decision then click
Decision:

Approximate C9 as a short-circuit.

3.4. Step 3

Don’t forget to redraw the circuit!

3.5. Step 4

Replace the transistor with its small-signal (hybrid-π) model. Tourbook: §6.4 Small-signal models

Then redraw the circuit a final* time.

1. Big Fat Capacitors
2. GND, but it is way too easy to get confused about (non-)magical ground nodes.