op amps are great, but they’re not perfect

1. note

Observation about the circuit analysis algebra from the end of (next time’s) day25. When analyzing a circuit with reactive components, it is helpful to know what to expect about the transfer function’s form. In general:

  • If there are N reactive components, then

  • the transfer function will have Nth-order polynomials in s for the numerator and denominator.
    → Example: 3 capacitors + 0 inductors = 3rd-order polynomials

For a real amplifier, the denominator has a the same or higher order than the numerator. This indicates that the gain eventually approaches zero as the frequency increases — 

Why does this make sense? (think, then click to reveal)

An amplifier can’t have infinite bandwidth and therefore must “roll off” eventually.

2. Operational amplifer DC errors

2.1. Review and ideal version

The textbook used for (my version of) ECE 264 (syllabus) is pretty decent, and intentionally zero cost from the authors. Its Chapter 4 on Operational Amplifiers is pretty good for an introduction and review.

The properties of an ideal op amp are:

  • Infinite input resistance.

  • Infinite gain.

  • Zero output resistance.

which then imply the following identities for circuit analysis:

  1. zero input current into each pin

  2. \(v_+ = v_-\) [1]

You should have studied ideal op amps some in ECE 264, but it will be worth your time to read through Chapter 4 of the Ulaby book.

2.2. DC errors

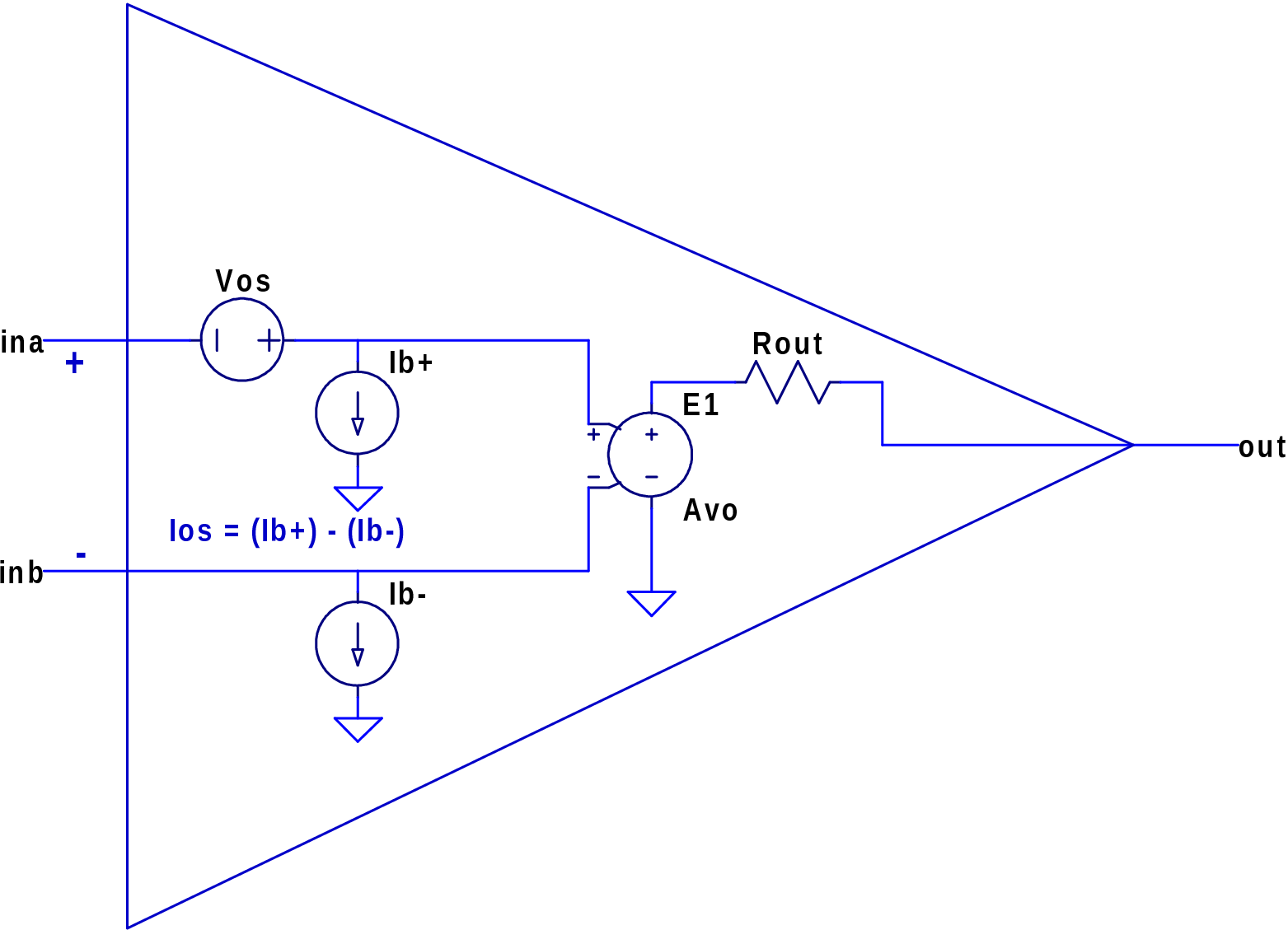
discrete opamp3 fig3
Figure 1. Op amp internal DC model

Figure 1 shows a schematic version of how these datasheet parameters affect the circuit’s behavior.

The major DC errors in a real op amp are:

  • Input offset voltage (Vos)

  • Input bias current (Ib)

  • Input offset current (Ios)

Plus transfer function terms (at 0 Hz or DC):

  • Open-circuit voltage gain (Av0)

  • Output impedance (Rout)

Use the circuits of Figure 2 and your measurements from Lab 5 to figure out these parameters for your op amp.

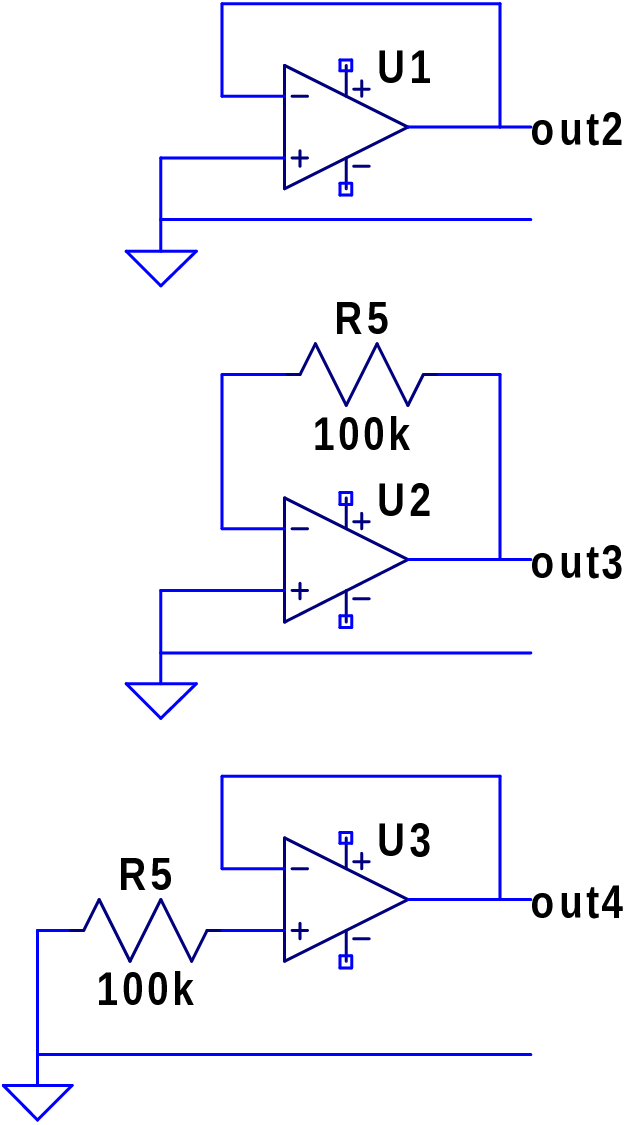
discrete opamp3 fig2
Figure 2. Lab 5 circuits

In Lab 5 you made an operational amplifier, pretty neat! The wacky circuits with the 100k resistor? They help you measure most of the major opamp parameters.

Find V(out2) using symbolic (linear) circuit analysis:

Find V(out3) using symbolic (linear) circuit analysis:

















Find V(out4) using symbolic (linear) circuit analysis:

















3. Datasheets are Life

day25_opamp-datasheets.pdf
opamp datasheet quiz

1. Though the two pins are the same voltage, they are not the same node, and so there are two separate KCLs at the two input nodes.